Hypercorrelation Squeeze for Few-Shot Segmentation
.
2021 paper
Juhong Min
Dahyun Kang
Minsu Cho
Abstract
Few-shot semantic segmentation은 query image에서 target object를 segment하는것을 오직 target class의 few annotated support images만 사용하여 learning하는것을 목표로 한다.
이 challenging task는 visual cues의 다양한 수준을 이해하고 query와 support images사이의 fine-grained correspondence relations를 분석하는것을 요구한다.
이 문제를 다루기 위해서, 우리는 multi-level feature correlation과 efficient 4D convolutions를 leverage하는 Hypercorrelation Squeeze Networks (HSNet)를 제안한다.
그것은 intermediate convolutional layers의 different levels로 부터 다양한 features를 extract하고 4D correlation tensors의 집합,즉, hypercorrelations을 construct한다.
pyramidal architecture에서 efficient center-pivot 4D convolutions을 사용하면, method는 점차적으로 hypercorrelation의 high-level semantic과 low-level geometric cues에서 정확한 segmentation masks로 coarse-to-fine방법으로 squeeze한다.
PASCAL-5, COCO-20, Fss-1000의 standard few-shot segmentation benchmarks를 상당히 향상한 performance를 통해 제안한 method의 효율성을 증명하였다.
1. Introduction
deep convolutional neural networks [17, 20, 64]의 도래는 to name a few(몇가지 예를들어) object tracking [28, 29, 45], visual correspondence [22, 44, 48], 그리고 semantic segmentation [7, 47, 62]를 포함해서 많은 computer vision tasks에 극적은 진보를 촉진해왔다. deep networks의 효율성에도 불구하고, data labeling은 실질적으로 사람의 노력이 필요하기 때문에 large-scale datasets [9, 11, 35]에 많은 양의 annotated examples의 수요가 여전히 근본적인 한계로 남아있다, 특히 dense prediction tasks, 예를들면 semantic segmentation.
challenge에 대체하기위해, 우리는 data-hunger issue를 효율적으로 완화하는 semi-, weakly-supervised segmentation approaches [6,26,39,66,72,77,88]등의 다양한 시도를 해왔다.
그러나, 오직 few annotated training examples만 주어졌을때, deep networks의 poor generalization ability의 문제는 많은 few-shot segmentation methods [10, 12, 13, 19, 33, 36, 37, 46, 54, 61, 63, 69, 70, 74, 75, 80, 83, 86, 87, 89]가 다룰려고 열심히 발버둥치는 주된 관심사는 아직 아니다. 대조적으로, human visual system은 extremely limited supervision 상황에서 새 objects의 appearance를 쉽게 generalizing을 성취한다. 이런 itelligence의 정점은 같은 class의 서로다른 instances에 신뢰할 만한 correspondences를 찾는 능력에 있다.
최근 semantic correspondence에 대한 연구는 leveraging dense intermediate features [38, 42, 44]와 processing correlation tensors with high-dimensional convolutions [30, 58, 71]은 정확한 correspndences를 성립하는데 상당히 효과적임을 보여준다.
그러나, 최근 few-shot segmentation 연구는 correlation learning 방향으로 활발한 탐사가 시작되었다, [36, 37, 46, 65, 73, 75, 80]들 대부분은 CNN의 초기부터 후반 layers까지 feature representations의 다양한 levels를 활용하는것도 fine-grained correlation patterns를 포착하기위해 pair-wise feature correlations를 구성하는것도 하지 않는다.
본 논문에서, 우리는 2개의 most influential techniques
이 연구에서 우리는 visual correspondence, multi-level features, 4D convolutions의 최근 연구에서 가장 영향력 있는 두 가지 기술을 결합하고 few-shot semantic segmentation의 task를 위해, 새로운 framework, dubbed Hypercorrelation Squeeze Networks (HSNet)를 디자인한다.
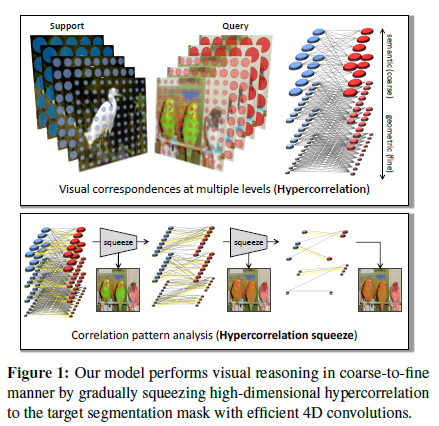
그림1을 보면 우리의 network는 많은 different intermediate CNN layers에서 다양한 geometric/semantic feature representations를 사용하여 4D correlation tensors의 집합 즉, multiple visual aspects 에 풍부한 correspondences의 집합을 represent하는 hypercorrelations를 구성한다.
FPN [34] 작업을 따르면, 우리는 deeply stacked 4D conv layers를 사용하여 coarse-to-fine 방법에서 정확한 mask prediction을 위해 pyramidal design을 high-level semantic과 low-level geometric cues 모두를 포착하게 조정한다.
high dimensional convs의 사용이 원인이 되는 computational burden를 줄이기 위해, 우리는 기존보다 더 효과적이고 더 light-weight한 real-time inference를 가능하게하는 합리적인 weight-sparsification을 통해 효과적인 4D kernel을 궁리한다.
PASCAL-5, COCO-20, FSS-1000이 standard few-shot segmentation benchmarks에 대한 향상은 우리의 method의 효과가 있음을 증명한다.
2. Related Work
Semantic segmentation
Few-shot learning
Learning visual correspondences
본 논문에서, 우리는 few-shot segmentation을 다루기위해 visual correspondence에서 가장 영향력 있는 2개의 methodologies: multi-level features와 4D convolutions을 조정한다.
효과적으로 “appearance features”를 build 하기위해 multi-level features를 사용하는 이전 matching methods [42,44,27]에 영감을 받아, 우리는 intermediate CNN features를 사용하여 high-dimensional “relational features”를 구성하고 그것들을 일련의 4D convolutions로 처리한다. 그러나 quadratic complexity은 여전히 cost-effective deep networks를 설계하는 데 있어 주요 bottleneck 현상으로 남아 있어 이전의 많은 matching methods가 몇 개의 4D conv layers만 사용하도록 제한한다. 이런 이슈를 해결하기 위해, 우리는 effective pattern recognition을 위해 vital parameters의 작은 하위 집합만 수집하여 light-weight 4D convolutional kernel을 개발하며, 이는 결국 linear complexity을 가진 한 쌍의 2D conv kernels로 효율적으로 분해된다.
우리의 contribution은 다음과 같이 요약할 수 있다:
deeply stacked 4D conv layers를 사용하여 diverse visual aspects의 dense feature matches를 분석하는 Hypercorrelation Squeeze Networks를 제안한다.
real-time inference를 성취하는 정확도와 속도 부분에서 기존것보다 더 효과적인 center-pivot 4D conv kernel를 제안한다.
제안된 method는 3개의 표준 few-shot segmentation benchmarks : PASCAL-5, COCO-20, FSS-1000에 새 sota를 세웠다.
3. Problem Setup
few-shot semantic segmentation의 목표는 오로지 few annotated examples만 주어졌을때 segmentation을 수행하는것이다.
insufficient training data때문에 overfitting의 risk를 피하기 위해, 우리는 넓게 사용되는 episodic training이라 불리는 metha-learning approach를 채택하였다.
object classes에 관련하여 분리된 각 training sets와 test sets를 \(\mathcal{D}_{\text{train}}\)와 \(\mathcal{D}_{\text{test}}\)로 나타내자. 두개 sets 모두 multiple episodes로 이루어져있고 각각은 a support set \(\mathcal{S} = (I^s, \mathbf{M}^s)\)와 query set \(\mathcal{Q} = (I^q, \mathbf{M}^q)\)로 구성되어있다, 여기서 \(I^*\)와 \(M^*\)는 각각 image와 그것의 corresponding mask label이다. training하는동안, 우리의 model은 \(\mathcal{D}_{\text{train}}\)에서 episode를 반복적으로 샘플링하고 \((I^s,M^s,I^q)\)에서 query mask \(\text{M}^q\)까지 매핑하는 것을 learn한다.
일단 모델이 trained되면, 그것은 further optimization없이 evaluation하기위해 learned mapping을 사용한다, 즉, model은 query mask를 predict하기위해 \(\mathcal{D}_{test}\)에서 랜덤하게 sampled된 \((I^s, \text{M}^s, I^q)\)를 가져오다.
4. Propsed Approach
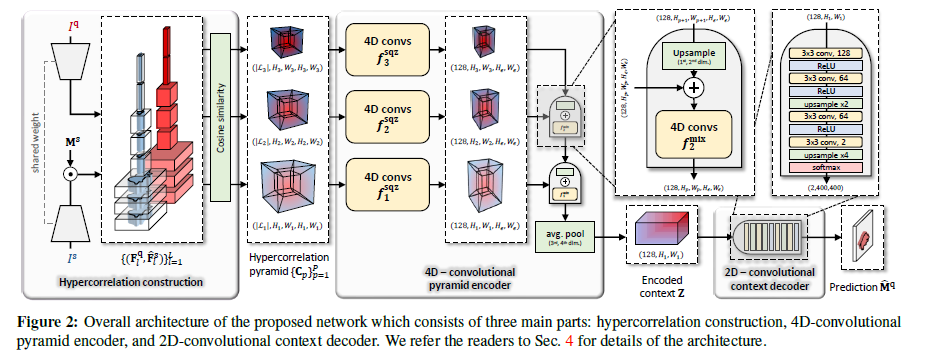
본 섹션에서, 우리는 novel few-shot segmentation architecture, 이것은 query image에서 fine-grained segmentation mask를 predict하기위해 a pair of input images간의 multi-level feature correlations에 관련있는 patterns를 capute하는 Hypercorrelation Squeeze Networks (HSNet)를 제안한다. 그림2에서 보듯, 우리는 우리 architecture안에서 encoder-decoder structure를 채택했다; encoder는 그것들의 local information을 global context에 취합함으로써 input hypercorrelations의 dimension을 점진적으로 squeezes한다. 그리고 query mask를 predict하기위해 decoder는 encoded context를 거친다.
Sec 4.1-4.3에서, 우리는 one-shot setting에서 각 pipeline을 시연한다, 즉 model은 \(I^q\)와 \(\mathcal{S}=(I^s, \mathbf{M}^s)\)가 주어지면 query mask를 predicts한다.
Sec. 4.4에서, 4D convs의 large resource demands를 완화시키기 위해, 우리는 memory와 time 모두에 관해서 model을 효과적으로 상당히 향상시킨 light-weight 4D kernel를 제안한다.
Sec. 4.5에서, 우리는 어떻게 model이 쉽게 K-shot setting으로 확장될 수 있는지 보여준다, 즉 \(\mathcal{S}=\{(I^s_k,\mathbf{M}^s_k)\}^K_{k=1}\), without loss of generality.
4.1 Hypercorrelation construction
최근 semantic matching approaches [38,42,44]에 영감을 받아, 우리의 모델은 support와 query images 사이의 similarities의 multi-level semantic과 geometric patterns을 capute하기 위해 convolutional neural network의 intermediate layers로 부터 a rich set of features를 이용한다.
query와 support images 쌍, \(I^q,I^s \in \mathbb{R}^{3 \times H \times W}\),가 주어지면, backbone network는 intermediate feature maps의 \(L\) pairs의 sequence \(\{(\mathbf{F}^q_l, \mathbf{F}^s_l)\}^L_{l=1}\)를 생성한다.
reliable mask prediction을 위해 우리는 support mask \(\mathbf{M}^s \in \{0,1\}^{H \times W}\)를 사용하여 각 support feature map \(\mathbf{F}^s_l \in \mathbf{R}^{C_l \times H_l \times W_l}\)을 mask해서 irrelevant activations을 버린다: \[\hat{\mathbf{F}}^s_l = \mathbf{F}^s_l \odot \zeta_l(\mathbf{M}^s), \tag{1}\]
여기서 \(\odot\)은 Hadamard product,
\(\zeta_l(\cdot)\)은 input tensor를 layer \(l\)에 feature map \(\mathbf{F}^s_l\)의 spatial size에 bilinearly interpolates하고 뒤이어 \(\zeta_l : \mathbb{R}^{H \times W} \rightarrow \mathbb{R}^{C_l \times H_l \times W_l}\)와 같은 channel dimension에 따른 확장하는 function이다.
subsequent hypercorrleation construction을 위해, 각 layer에 query와 masked support features의 pair는 cosine similarity를 사용하여 4D correlation tensor \(\hat{\mathbf{C}}_l \in \mathbb{R}^{H_l \times W_l \times H_l \times W_l}\) 를 형성한다: \[\hat{\mathbf{C}}_l(\mathbf{x}^q, \mathbf{x}^s) = \text{ReLU} \left ( \frac{\mathbf{F}^q_l(\text{x}^q) \cdot \hat{\mathbf{F}}^s_l(\text{x}^s)}{||\mathbf{F}^q_l(\text{x}^q)|| ||\hat{\mathbf{F}}^s_l(\text{x}^s)||} \right ) \tag{2}\]
\(\text{x}^q\)와 \(\text{x}^ㄴ\)는 각각의 feature maps \(\mathbf{F}^q_l\)과 \(\hat{\mathbf{F}}^s_l\)의 2-dimensional spatial positions를 나타내고
ReLU는 noisy correlation scores를 억누른다.
resultant set of 4D correlations \(\{ \hat{\mathbf{C}_l} \}^L_{l=1}\) 로 부터, 우리는 4D tensors를 모은다, 만일 그것들이 same spatial sizes를 갖는다면. subset을 \(\{ \hat{\mathbf{C}_l} \}_{l \in \mathcal{L}_p}\)로 나타낸다, \(\mathcal{L}_p\)는 pyramidal layer \(p\)에 CNN layer 집합의 indices \(\{1, ..., L\}\). 최종적으로, \(\{\hat{\mathbf{C}}_l\}_{l\in\mathcal{L}_p}\)에 모든 4D tensors는 channel dimension을 따라 concatenated되어 hypercorrelation \(\mathbf{C}_p \in \mathbb{R}^{|\mathcal{L}_p| \times H_p \times W_p \times H_p \times W_p}\)를 형성한다, 여기서 \((H_p,W_p,H_p,W_p)\)는, 표기를 남용하여, pyramidal layer \(p\)에 hypercorrelation의 spatial resolution을 represents한다.
\(P\) pyramidal layers를 고려하면, 우리는 hypercorrelation pyramid를 \(\mathcal{C} = \{ \mathbf{C}_p \}^P_{p=1}\)로 표기한다, 이것은 multiple visual aspects에서 a rich collection of feature correlations를 representing한다.
4.2. 4D-convolutional pyramid encoder
우리의 encoder network는 hypercorrelation pyramid \(\mathcal{C} = \{ \mathbf{C}_p \}^P_{p=1}\)를 사용하여 condensed feature map \(\mathbf{F} \in \mathbb{R}^{128 \times H_1 \times W_1}\)에 효과적으로 squeeze한다. 우리는 two types of building blocks: squeezing block \(f^{sqz}_p\)와 mixing block \(f^{mix}_p\)을 사용하여 correlation learning를 성취한다.
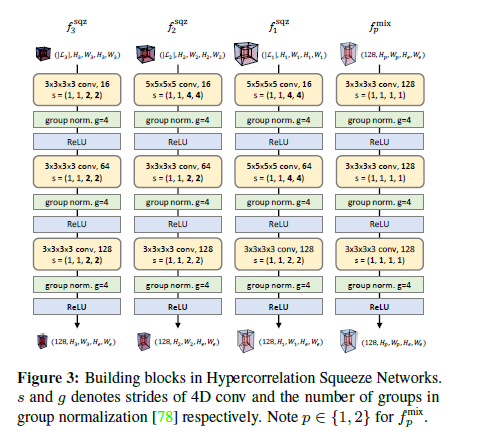
각 block은 multi-channel 4D convolution, group normalization [78], 그리고 ReLU activation 이렇게 한 세트로 3개의 sequences로 구성되어 있다 (그림3 참고).
squeezing block \(f^{sqz}_p\) 안에서, large strides는 주기적으로 \(\mathbf{C}_p\)의 last two (support) spatial dimensions를 \((H_{\epsilon},W_{\epsilon})\)으로 낮춰 squeeze하고 반면 first two spatial (query) dimensions은 \((H_p,W_p)\)로 같게 유지한다,
| 즉 $$f^{sqz}_p : \mathbb{R}^{ | \mathcal{L}_p | \times H_p \times W_p \times H_p \times W_p} \rightarrow \mathbb{R}^{128 \times H_p \times W_p \times H_{\epsilon} \times W_{\epsilon}}$$ |
여기서 \(H_p > H_{\epsilon}\) and \(W_p > W_{\epsilon}\).
FPN [34] structure와 유사하게, adjacent pyramidal layers에 2개의 outputs, \(p\)와 \(p+1\)은 upper layer output의 (query) spatial dimensions를 upsampling이후 element-wise addition으로 통합된다.
그런 다음 mixing block \(f^{\text{mix}}_p : \mathbb{R}^{128 \times H_p \times W_p \times H_{\epsilon} \times W_{\epsilon}} \rightarrow \mathbb{R}^{128 \times H_p \times W_p \times H_{\epsilon} \times W_{\epsilon}}\)은 이 mixture을 4D convolutions을 사용하여 하향식 방식(top-down fashion)으로 relevant information를 lower layers에 propagate한다.
iterative propagation이후, lowest mixing block \(f^{\text{mix}}_1\)의 output tensor는 its last two (support) spatial dimensions를 average-pooling함으로써 더욱 압축된다, hypercorrelation \(\mathcal{C}\)의 condensed representation을 상징하는 2-dimensional feature map \(\mathbf{Z} \in \mathbb{R}^{128 \times H_1 \times W_1}\)을 차례로 제공한다.
4.3. 2D-convolutional context decoder
series of 2D convolutions, ReLU, 그리고 softmax function을 따르는 upsampling layers로 구성되어있다. (그림 2확인)
network는 context representation \(\mathbf{Z}\)를 가져오고 two-channel map \(\hat{\mathbf{M}}^q \in [0,1]^{2 \times H \times W}\)를 predict한다.(여기서 two channel values는 foreground와 background의 probabilities를 표기함)
training동안, network parameters는 모든 pixel localtion에 걸쳐 prediction \(\hat{\mathbf{M}}^q\)와 ground-truth \(\mathbf{M}^q\)간의 mean of cross-entropy loss를 이용해 optimized된다.
testing하는동안, 우리는 평가를 위한 final query mask prediction \(\bar{\mathbf{M}}^q \in {0,1}^{H \times W}\)을 얻기 위해 각 pixel에서 maximum channel value를 취한다.
4.4. Center-pivot 4D convolution
분명히, 그렇게 많은 4D convolutions을 가진 우리 network는 차원의 저주(curse of dimensionality)로 인해 상당한 양의 resources을 필요로 하는데, 이로 인해 많은 visual correspondence methods이 few 4D conv layers만 사용하도록 제한되었다.
우려를 해결하기 위해서, 우리는 4D convolution operation를 revisit하고 그것의 limitations을 파헤친다. 그런다음 우리는 어떻게 unique weight-sparsification scheme가 효과적으로 이 문제를 해결하는지를 보여준다.
4D convolution and its limitation
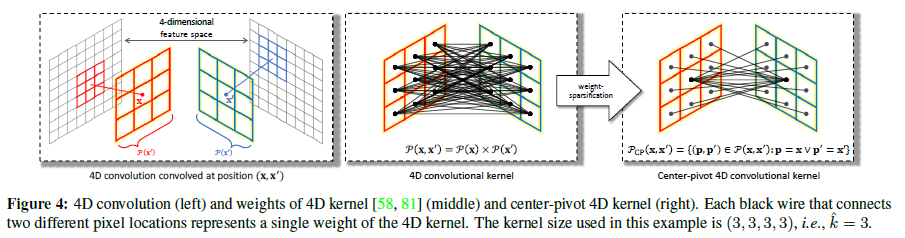
position \((\text{x}, \text{x}') \in \mathbb{R}^4\)에 correlation tensor \(c \in \mathbb{R}^{H \times W \times H \times W}\)에 kernel \(k \in \mathbb{R}^{\hat{k} \times \hat{k} \times \hat{k} \times \hat{k}}\)에 의해 parameterized된 전형적인 4D convolution은 다음과 같이 공식화 된다. \[(c * k)(\text{x}, \text{x}') = \sum_{(\mathbf{p},\mathbf{p}') \in \mathcal{P}(\text{x}, \text{x}')} c(\mathbf{p}, \mathbf{p}') k (\mathbf{p} - \text{x}, \mathbf{p}' - \text{x}'), \tag{3}\]
여기서 \(\mathcal{P}(\text{x}, \text{x}')\)는 position \((\text{x}, \text{x}')\)를 중심으로 하는 local 4D window안에 a set of neighbourhood regions를 나타낸다, 즉 \(\mathcal{P}(\text{x}, \text{x}') = \mathcal{P}(\text{x}) \times \mathcal{P}(\text{x}')\) 그림 4 참고.
correlation tensor에 4D convolutions을 사용하면 correspondence-related domains [22,30,32,58,71]에서 우수한 경험적 성능과 함께 그 효능이 입증되었지만, input features의 size와 관련된 quadratic complexity은 여전히 주요 bottleneck 현상으로 남아 있다.
또 다른 limiting factor은 high-dimensional kernel의 over-parameterization이다: \(n\text{D}\) conv kernel에 의해 convolved된 \(n\text{D}\) tensor에서의 single activation를 고려해보자.
kernel이 이 activation을 처리하는 횟수는 \(n\)에 기하급수적으로 비례한다.
이는 magnitudes가 큰 unreliable input activations가 high-dimensional kernel에 과도하게 노출되어 reliable patterns을 캡처하는 데 noise를 수반할 수 있음을 의미한다.
[81]의 연구는 공간적으로 분리 가능한 4D kernels을 사용하여 후자의 문제(numerical instability)를 해결하는 additional batch normalization layers [23]과 함께 두 개의 분리된 2D kernels을 사용하여 4D conv을 approximate하기 위해 이전 문제(quadratic complexity)를 해결한다.
이 작업에서 우리는 동시에 문제들을 다루기 위해 novel weight-sparsification scheme를 소개한다.
Center-pivot 4D convolution