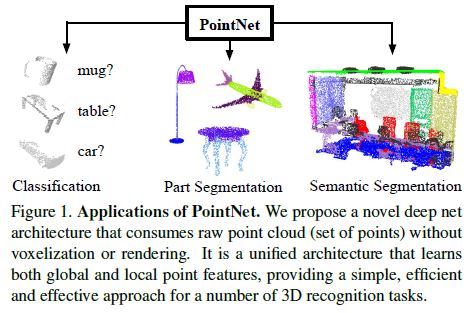
PointNet
: Deep Learning on Point Sets for 3D Classification and Segmentation
2017 CVPR code : tensorflow pytorch
Abstract
Point cloud is an important type of geometric data structure.
Due to its irregular format, most researchers transform such data to regular 3D voxel grids or collections of images.
This, however, renders data unnecessarily voluminous and causes issues.
In this paper, we design a novel type of neural network that directly consumes point clouds, which well respects the permutation invariance of points in the input.
Point cloud는 geometric data structure의 중요한 유형이다.
irregular format으로 인해 대부분의 연구자들은 이러한 데이터를 일반 3D voxel grids 또는 collections of images으로 변환한다.
그러나 이것은 데이터를 불필요하게 voluminous하게 생성되고 문제가 발생한다.
본 논문에서, 우리는 point clouds를 직접 사용하는 새로운 유형의 neural network을 설계하는데, 이는 입력에서 points의 permutation invariance을 잘 보존한다.
Our network, named PointNet, provides a unified architecture for applications ranging from object classification, part segmentation, to scene semantic parsing.
Though simple, PointNet is highly efficient and effective.
Empirically, it shows strong performance on par or even better than state of the art.
PointNet이라는 이름의 우리 network는 object classification, part segmentation, scene semantic parsing에 이르는 applications을 위한 통합 아키텍처를 제공한다. PointNet은 간단하지만 매우 효율적이고 효과적이다. 경험적으로, 그것은 최신것보다 동등하거나 훨씬 더 나은 성능을 보여준다.
Theoretically, we provide analysis towards understanding of what the network has learnt and why the network is robust with respect to input perturbation and corruption.
이론적으로, 우리는 네트워크가 학습한 내용과 input perturbation 및 corruption과 관련하여 네트워크가 robust한 이유를 이해하기 위한 분석을 제공한다.
1. Introduction
In this paper we explore deep learning architectures capable of reasoning about 3D geometric data such as point clouds or meshes.
Typical convolutional architectures require highly regular input data formats, like those of image grids or 3D voxels, in order to perform weight sharing and other kernel optimizations.
본 논문에서는 point clouds나 meshes와 같은 3D geometric data에 대해 추론할 수 있는 deep learning architectures를 탐구한다. 일반적인 convolutional architectures는 weight sharing 및 other kernel optimizations를 수행하기 위해, image grids 또는 3D voxels과 같은 매우 규칙적인 input data formats이 필요하다.
Since point clouds or meshes are not in a regular format, most researchers typically transform such data to regular 3D voxel grids or collections of images (e.g, views) before feeding them to a deep net architecture. This data representation transformation, however, renders the resulting data unnecessarily voluminous while also introducing quantization artifacts that can obscure natural invariances of the data.
point clouds 또는 meshes는 regular format이 아니기 때문에, 대부분의 연구자들은 일반적으로 이러한 데이터를 deep net architecture에 공급하기 전에 regular 3D voxel grid 또는 collections of images(예: views)으로 변환한다.
그러나 이러한 data representation transformation은 결과 데이터를 불필요하게 voluminous하게 만드는 동시에 데이터의 natural invariances을 모호하게 할 수 있는 quantization artifacts를 도입한다.
For this reason we focus on a different input representation for 3D geometry using simply point clouds – and name our resulting deep nets PointNets.
Point clouds are simple and unified structures that avoid the combinatorial irregularities and complexities of meshes, and thus are easier to learn from.
이러한 이유로 우리는 단순히 point clouds를 사용하는 3D geometry에 대한 다른 input representation에 초점을 맞추고, 결과적인 deep nets의 이름을 PointNets로 지정한다.
Point clouds는 meshes의 combinatorial irregularities and complexities을 피하는 단순하고 통합된 구조이므로 쉽게 학습 할 수 있다.
The PointNet, however, still has to respect the fact that a point cloud is just a set of points and therefore invariant to permutations of its members, necessitating certain symmetrizations in the net computation.
Further invariances to rigid motions also need to be considered.
그러나 PointNet은 point cloud가 단지 points의 집합이므로 point들의 permutations에는 invariant한다는 사실을 존중해야 하며, net computation에서 certain symmetrizations가 필요하다. rigid motions에 대한 추가 invariances도 고려할 필요가 있다.
Our PointNet is a unified architecture that directly takes point clouds as input and outputs either class labels for the entire input or per point segment/part labels for each point of the input.
The basic architecture of our network is surprisingly simple as in the initial stages each point is processed identically and independently.
In the basic setting each point is represented by just its three coordinates (x, y, z).
Additional dimensions may be added by computing normals and other local or global features.
우리의 PointNet은 point clouds를 input으로 직접 가져오고 전체 input에 대한 class labels 또는 input의 각 point에 대한 point segment/part labels을 출력하는 통합 architecture이다. 우리 network의 basic architecture는 초기 단계에서 각 지점이 동일하고 독립적으로 처리되기 때문에 놀라울 정도로 간단하다. 기본 설정에서 각 point은 세 개의 좌표(x, y, z)로만 표시된다. 표준 및 other local 또는 global features을 계산하여 additional dimensions을 추가할 수 있다.
Key to our approach is the use of a single symmetric function, max pooling.
Effectively the network learns a set of optimization functions/criteria that select interesting or informative points of the point cloud and encode the reason for their selection.
The final fully connected layers of the network aggregate these learnt optimal values into the global descriptor for the entire shape as mentioned above (shape classification) or are used to predict per point labels (shape segmentation).
우리의 접근 방식의 핵심은 single symmetric function인 max pooling의 사용이다. network는 point cloud의 interesting 하거나 informative한 points를 선택하고 선택 이유를 인코딩하는 일련의 optimization functions/criteria을 효과적으로 학습한다. network의 final fully connected layers는 위에서 언급한(shape classification) 전체 shape에 대해 학습된 optimal values을 global descriptor로 집계하거나 point labels (shape segmentation)을 예측하는 데 사용된다.
Our input format is easy to apply rigid or affine transformations to, as each point transforms independently. Thus we can add a data-dependent spatial transformer network that attempts to canonicalize the data before the PointNet processes them, so as to further improve the results.
우리의 input format은 각 point이 독립적으로 변환될 때, rigid되거나 affine transformations을 적용하기가 쉽다. 따라서 우리는 PointNet이 데이터를 처리하기 전에, 데이터를 canonicalize를 시도하는 data-dependent spatial transformer network를 추가하여 결과를 더욱 개선할 수 있다.
We provide both a theoretical analysis and an experimental evaluation of our approach.
We show that our network can approximate any set function that is continuous.
More interestingly, it turns out that our network learns to summarize an input point cloud by a sparse set of key points, which roughly corresponds to the skeleton of objects according to visualization.
The theoretical analysis provides an understanding why our PointNet is highly robust to small perturbation of input points as well as to corruption through point insertion (outliers) or deletion (missing data).
우리는 우리의 접근 방식에 대한 이론적 분석과 실험 평가를 제공한다. 우리는 우리의 network가 연속적인 모든 설정 함수에 근사할 수 있다는 것을 보여준다. 더 흥미롭게도, 우리 network는 시각화에 따르는 skeleton of objects에 roughly하게 해당하는 a sparse set of key points으로 input point cloud를 요약하는 방법을 학습하는 것으로 밝혀졌다.
이론적 분석은 우리의 PointNet이 왜 small perturbation of input points뿐만 아니라 point insertion (outliers) 또는 deletion (missing data)를 통한 손상에도 매우 robust한지 증명한다.
On a number of benchmark datasets ranging from shape classification, part segmentation to scene segmentation, we experimentally compare our PointNet with state-ofthe-art approaches based upon multi-view and volumetric representations.
Under a unified architecture, not only is our PointNet much faster in speed, but it also exhibits strong performance on par or even better than state of the art.
shape classification, part segmentation, scene segmentation에 이르는 많은 benchmark datasets에서, 우리는 multi-view 및 volumetric representations을 기반으로 하는 최신 접근 방식과 우리의 PointNet을 실험적으로 비교한다.
unified architecture에서는 PointNet의 속도가 훨씬 빠를 뿐만 아니라 최신 기술에 비해 성능이 우수하다.
The key contributions of our work are as follows:
- We design a novel deep net architecture suitable for consuming unordered point sets in 3D;
- We show how such a net can be trained to perform 3D shape classification, shape part segmentation and scene semantic parsing tasks;
- We provide thorough empirical and theoretical analysis on the stability and efficiency of our method;
- We illustrate the 3D features computed by the selected neurons in the net and develop intuitive explanations for its performance.
주요 기여
- unordered point sets를 3D로 사용하기에 적합한 새로운 deep net architecture를 설계
- 우리는 이러한 net이 3D shape classification, shape part segmentation 및 scene semantic parsing tasks을 수행하기 위해 어떻게 훈련될 수 있는지 보여줌.
- 방법의 안정성 및 효율성에 대한 철저한 경험적, 이론적 분석을 제공.
- 선택된 neuron들이 net에서 계산한 3D features을 설명하고 성능에 대한 직관적인 explanations을 개발한다.
The problem of processing unordered sets by neural nets is a very general and fundamental problem – we expect that our ideas can be transferred to other domains as well.
neural nets에 의한 unordered sets 처리 문제는 매우 일반적이고 근본적인 문제이다. 우리는 우리의 아이디어가 다른 영역으로 옮겨질 수 있을 것으로 기대한다.
2. Related Work
Point Cloud Features
Most existing features for point cloud are handcrafted towards specific tasks.
Point features often encode certain statistical properties of points and are designed to be invariant to certain transformations, which are typically classified as intrinsic [2, 24, 3] or extrinsic [20, 19, 14, 10, 5].
They can also be categorized as local features and global features. For a specific task, it is not trivial to find the optimal feature combination.
point cloud의 기존 features은 대부분 특정 작업을 위해 수작업으로 제작된다. Point features은 종종 points의 certain statistical properties을 인코딩하고 certain transformations에 invariant하도록 설계되며, 일반적으로 본질적인 [2, 24, 3] 또는 외적인 [20, 19, 14, 10, 5]로 분류된다. 또한 local features과 global features으로 분류할 수 있다. 특정 작업의 경우, optimal feature combination을 찾는 것이 사소한 일이 아니다.
Deep Learning on 3D
3D data has multiple popular representations, leading to various approaches for learning.
3D 데이터는 여러 가지 인기 있는 representations을 가지고 있어 학습을 위한 다양한 접근 방식으로 이어진다.
Volumetric CNNs: [28, 17, 18] are the pioneers applying 3D convolutional neural networks on voxelized shapes.
However, volumetric representation is constrained by its resolution due to data sparsity and computation cost of 3D convolution.
Volumetric CNNs: [28, 17, 18]은 voxel화된 shapes에 3D convolutional neural networks을 적용하는 선구자이다. 그러나 volumetric representation은 data sparsity과 3D convolution의 계산 비용 때문에 해상도에 의한 제약을 받는다.
FPNN [13] and Vote3D [26] proposed special methods to deal with the sparsity problem; however, their operations are still on sparse volumes, it’s challenging for them to process very large point clouds.
FPNN[13]과 Vote3D[26]는 sparsity problem를 다루기 위한 특별한 방법을 제안했지만, 작업은 여전히 sparse volumes에서 이루어지기 때문에, 매우 큰 point clouds를 처리하는 것은 어렵다.
Multiview CNNs: [23, 18] have tried to render 3D point cloud or shapes into 2D images and then apply 2D conv nets to classify them.
With well engineered image CNNs, this line of methods have achieved dominating performance on shape classification and retrieval tasks [21].
However, it’s nontrivial to extend them to scene understanding or other 3D tasks such as point classification and shape completion.
Multiview CNNs: [23, 18]은 3D point cloud 또는 shapes을 2D images으로 렌더링한 다음, 2D conv nets를 적용하여 분류하려고 시도했다. 잘 설계된 이미지 CNN을 통해 이 일련의 방법은 shape classification 및 retrieval tasks에서 지배적인 성능을 달성했다[21].
그러나 scene understanding 또는 point classification 및 shape completion.와 같은 다른 3D tasks으로 확장하는 것에 중점을 두고 있지 않다.
Spectral CNNs: Some latest works [4, 16] use spectral CNNs on meshes.
However, these methods are currently constrained on manifold meshes such as organic objects and it’s not obvious how to extend them to non-isometric shapes such as furniture.
Spectral CNNs: 일부 latest works [4, 16]은 meshes에 spectral CNNs을 사용한다.
하지만, 이러한 방법들은 현재 organic objects과 같은 여러 meshes에 제한되며, 어떻게 그것들을 가구와 같은 non-isometric shapes으로 확장시킬지는 분명하지 않다.
Feature-based DNNs: [6, 8] firstly convert the 3D data into a vector, by extracting traditional shape features and then use a fully connected net to classify the shape.
We think they are constrained by the representation power of the features extracted.
Feature-based DNNs: [6, 8]은 먼저 전통적인 shape features을 추출하여, 3D data를 vector로 변환한 다음 fully connected net을 사용하여 shape을 분류한다.
우리는 그것들이 추출된 features의 representation power에 의해 제약을 받는다고 생각한다.
Deep Learning on Unordered Sets
From a data structure point of view, a point cloud is an unordered set of vectors.
While most works in deep learning focus on regular input representations like sequences (in speech and language processing), images and volumes (video or 3D data), not much work has been done in deep learning on point sets.
데이터 구조 관점에서, point cloud은 unordered set of vectors이다.
deep learning에서 대부분의 작업은 sequences(음성 및 언어 처리), images and volumes(비디오 또는 3D 데이터)와 같은 regular input representations에 초점을 맞추고 있지만, point sets에 대한 deep learning에서는 많은 작업이 수행되지 않는다.
One recent work from Oriol Vinyals et al [25] looks into this problem.
They use a read-process-write network with attention mechanism to consume unordered input sets and show that their network has the ability to sort numbers.
However, since their work focuses on generic sets and NLP applications, there lacks the role of geometry in the sets.
Oriol Vinyals 외 연구진[25]의 최근 연구는 이 문제를 조사한다. 그들은 attention mechanism이 있는 read-process-write network를 사용하여 unordered input sets를 사용하고 network가 숫자를 정렬할 수 있다는 것을 보여준다.
그러나 이들의 작업은 일반 sets와 NLP applications에 중점을 두기 때문에, sets에서 geometry 역할이 부족하다.
3. Problem Statement
We design a deep learning framework that directly consumes unordered point sets as inputs.
A point cloud is represented as a set of 3D points \(\{P_i|i = 1, ..., n\}\), where each point \(P_i\) is a vector of its \((x, y, z)\) coordinate plus extra feature channels such as color, normal etc.
For simplicity and clarity, unless otherwise noted, we only use the \((x, y, z)\) coordinate as our point’s channels.
우리는 unordered point sets를 inputs으로 직접 사용하는 deep learning framework를 설계한다.
point cloud은 3D points \(\{P_i|i = 1, ..., n\}\)의 집합으로 표현되며, 여기서 각 point \(P_i\)는 \((x, y, z)\) 좌표의 vector이며 color, normal 등과 같은 extra feature channels이다. 단순성과 명확성을 위해, 달리 명시되지 않은 한, 우리는 \((x, y, z)\) 좌표만 point의 채널로 사용한다.
For the object classification task, the input point cloud is either directly sampled from a shape or pre-segmented from a scene point cloud.
Our proposed deep network outputs \(k\) scores for all the \(k\) candidate classes.
For semantic segmentation, the input can be a single object for part region segmentation, or a sub-volume from a 3D scene for object region segmentation.
Our model will output \(n \times m\) scores for each of the \(n\) points and each of the \(m\) semantic subcategories.
object classification task의 경우, input point cloud는 shape에서 직접 샘플링되거나 scene point cloud에서 pre-segmented 된다.
제안된 deep network는 모든 \(k\) 후보 클래스에 대해 \(k\) 점수를 출력한다.
semantic segmentation의 경우, 입력은 part region segmentation을 위한 single object이거나 object region segmentation을 위한 3D scene의 sub-volume일 수 있다.
우리의 model은 각 \(n\) points와 각 \(m\) semantic subcategories에 대해 \(n \times m\) scores를 출력한다.
4. Deep Learning on Point Sets
The architecture of our network (Sec 4.2) is inspired by the properties of point sets in \(\mathbb{R}^n\) (Sec 4.1).
우리 network의 architecture는 properties of point sets in \(\mathbb{R}^n\) (Sec 4.1)에서 영감을 받았다.
4.1. Properties of Point Sets in \(\mathbb{R}^n\)
Our input is a subset of points from an Euclidean space.
It has three main properties:
- Unordered.
Unlike pixel arrays in images or voxel arrays in volumetric grids, point cloud is a set of points without specific order.
In other words, a network that consumes \(N\) 3D point sets needs to be invariant to \(N!\) permutations of the input set in data feeding order.
Unordered.
images에서 pixel arrays 또는 volumetric grids에서 voxel arrays과 달리, point cloud는 특정 순서가 없는 points 집합이다.
즉, \(N\) 3D point sets를 사용하는 network는 데이터 공급 순서로 input set의 \(N!\) permutations에 invariant해야 한다.
- Interaction among points.
The points are from a space with a distance metric.
It means that points are not isolated, and neighboring points form a meaningful subset.
Therefore, the model needs to be able to capture local structures from nearby points, and the combinatorial interactions among local structures.
Interaction among points.
points은 distance metric이 있는 space에서 가져온 것이다.
즉, points가 분리되지 않고 neighboring points이 의미 있는 부분 집합(subset)을 형성한다.
따라서 model은 nearby points에서 local structures를 포착할 수 있어야 하며, local structures 간의 combinatorial interactions을 포착할 수 있어야 한다.
- Invariance under transformations.
As a geometric object, the learned representation of the point set should be invariant to certain transformations.
For example, rotating and translating points all together should not modify the global point cloud category nor the segmentation of the points.
Invariance under transformations. geometric object로서, point set의 학습된 representation은 certain transformations에 invariant해야 한다.
예를 들어, points을 회전하고 변환하는 것은 global point cloud category나 points의 segmentation을 수정하지 않아야 한다.
4.2. PointNet Architecture
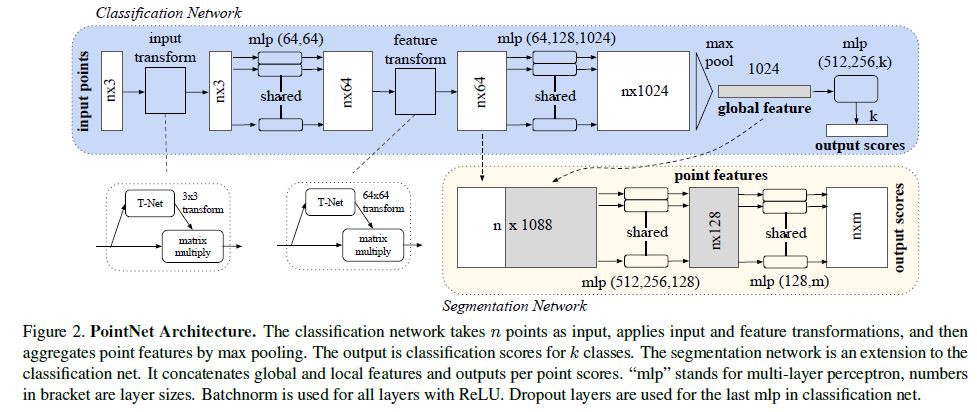
Our full network architecture is visualized in Fig 2, where the classification network and the segmentation network share a great portion of structures.
Please read the caption of Fig 2 for the pipeline.
우리의 full network architecture는 classification network와 segmentation network가 구조의 많은 부분을 공유한다. Fig 2에서 시각화하였다.
Our network has three key modules: the max pooling layer as a symmetric function to aggregate information from all the points, a local and global information combination structure, and two joint alignment networks that align both input points and point features.
우리의 network에는 세 가지 주요 모듈이 있다:
모든 points에서 information를 집계하는 symmetric function으로서의 max pooling layer,
local 및 global information 조합 구조,
input points와 point features을 모두 정렬하는 두 개의 공동 정렬 네트워크(two joint alignment networks).
We will discuss our reason behind these design choices in separate paragraphs below.
Symmetry Function for Unordered Input
In order to make a model invariant to input permutation, three strategies exist:
1) sort input into a canonical order;
2) treat the input as a sequence to train an RNN, but augment the training data by all kinds of permutations;
3) use a simple symmetric function to aggregate the information from each point.
input permutation에 invariant하는 model을 만들기 위해 다음과 같은 세 가지 전략이 존재한다. 1) canonical order로 입력을 정렬. 2) 입력은 RNN을 훈련시키는 sequence로 취급하되, 모든 종류의 permutations로 훈련 데이터를 증가. 3) 간단한 symmetric function를 사용하여 각 point에서 정보를 취합
Here, a symmetric function takes \(n\) vectors as input and outputs a new vector that is invariant to the input order.
For example, + and * operators are symmetric binary functions.
여기서 symmetric function는 n개의 vectors를 입력으로 받아들이고 입력 순서에 invariant하는 새로운 벡터를 출력한다. 예를 들어, + 및 * 연산자는 symmetric binary functions입니다.
While sorting sounds like a simple solution, in high dimensional space there in fact does not exist an ordering that is stable w.r.t. point perturbations in the general sense.
This can be easily shown by contradiction.
If such an ordering strategy exists, it defines a bijection map between a high-dimensional space and a \(1d\) real line.
반면 sorting이 간단한 solution처럼 보이지만, high dimensional space은 general sense에서 stable w.r.t. point perturbations 인 ordering이 존재하지 않는다.
이것이 contradiction에 의해 쉬워보일수 있다.
만약 그런 ordering strategy가 존재한다면, 그것은 high-dimensional space과 \(1d\) real line 사이의 bijection map을 정의한다.
It is not hard to see, to require an ordering to be stable w.r.t point perturbations is equivalent to requiring that this map preserves spatial proximity as the dimension reduces, a task that cannot be achieved in the general case.
stable w.r.t point perturbations을 위한 ordering을 요구하는 것은 일반적인 경우에서 달성할 수 없는 작업인 dimension reduces에 따라 map이 spatial proximity를 보존하도록 요구하는 것과 같다.
Therefore, sorting does not fully resolve the ordering issue, and it’s hard for a network to learn a consistent mapping from input to output as the ordering issue persists.
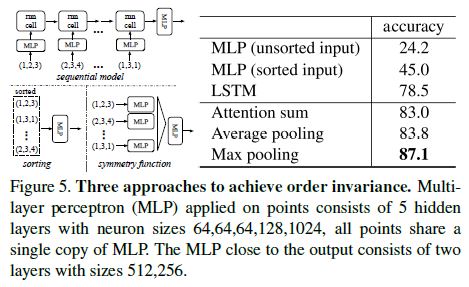
As shown in experiments (Fig 5), we find that applying a MLP directly on the sorted point set performs poorly, though slightly better than directly processing an unsorted input.
따라서 sorting을 해도 ordering issue가 완전히 해결되지 않으며, network가 ordering issue가 지속되면 input에서 output으로 일관된 mapping을 학습하기 어렵다.
실험(Fig 5)에서 볼 수 있듯이, 정렬된 point set에 직접 MLP를 적용하는 것은 정렬되지 않은 input을 직접 처리하는 것보다 약간 더 낫지만, 성능이 좋지 않다는 것을 발견했다.
The idea to use RNN considers the point set as a sequential signal and hopes that by training the RNN with randomly permuted sequences, the RNN will become invariant to input order.
However in “OrderMatters” [25] the authors have shown that order does matter and cannot be totally omitted.
While RNN has relatively good robustness to input ordering for sequences with small length (dozens), it’s hard to scale to thousands of input elements, which is the common size for point sets.
Empirically, we have also shown that model based on RNN does not perform as well as our proposed method (Fig 5).
RNN을 사용한다는 idea는 point 집합을 sequential signal로 간주하고 랜덤하게 permuted sequences로 RNN을 훈련시킴으로써 RNN이 input 순서에 invariant하게 될 것을 희망한다.
그러나 “OrderMatters”[25]에서 저자들은 order가 중요하며 완전히 생략할 수 없다는 것을 보여주었다.
RNN은 small length (dozens)를 가진 sequences에 대한 input 순서에서 상대적으로 우수한 robustness을 가지고 있지만, point 집합의 일반적인 size인, 수천 개의 입력 요소로 확장하기는 어렵다. 경험적으로, 우리는 또한 RNN 기반인 model이 우리가 제안한 방법만큼 성능이 좋지 않다는 것을 보여주었다(그림 5).
Our idea is to approximate a general function defined on a point set by applying a symmetric function on transformed elements in the set:
\[f({x_1, ... , x_n}) \approx g(h(x1), ... , h(x_n)), \qquad \qquad \qquad (1)\]우리의 idea는 집합에서 변환된 elements에 symmetric function를 적용하여 point 집합에 정의된 general function를 근사화하는 것이다:
where \(f : 2^{\mathbb{R}^N} \rightarrow \mathbb{R}^N, h : \mathbb{R}^N \rightarrow \mathbb{R}^K\) and \(g : \mathbb{R}^K x ... x \mathbb{R}^K \rightarrow \mathbb{R}\) is a synmmetric function.
Empirically, our basic module is very simple: we approximate \(h\) by a multi-layer perceptron network and \(g\) by a composition of a single variable function and a max pooling function.
This is found to work well by experiments.
Through a collection of \(h\), we can learn a number of f’s to capture different properties of the set.
경험적으로, 우리의 basic module은 매우 간단하다: 우리는 multi-layer perceptron network에 의한 \(h\)와 single variable function와 max pooling function의 구성에 의한 \(g\)를 근사화한다.
이것은 실험에 의해 효과가 있는 것으로 밝혀졌다.
a collection of \(h\)을 통해 우리는 집합의 다른 속성을 캡처하는 많은 f를 배울 수 있다.
While our key module seems simple, it has interesting properties (see Sec 5.3) and can achieve strong performace (see Sec 5.1) in a few different applications.
Due to the simplicity of our module, we are also able to provide theoretical analysis as in Sec 4.3.
우리의 key module은 단순해 보이지만, 흥미로운 properties을 가지고 있으며(Sec 5.3 참조) 몇 가지 다른 applications에서 강력한 성능을 달성할 수 있다.
모듈의 단순성 때문에, Sec 4.3와 같이 이론적 분석도 제공할 수 있다.
Local and Global Information Aggregation
The output from the above section forms a vector \([f_1, ... , f_K]\), which is a global signature of the input set.
We can easily train a SVM or multi-layer perceptron classifier on the shape global features for classification.
However, point segmentation requires a combination of local and global knowledge.
We can achieve this by a simple yet highly effective manner.
위의 섹션의 output은 input set의 global signature인 vector \([f_1, ... , f_K]\)를 형성한다.
우리는 classification를 위해 shape global features에 대한 SVM 또는 multi-layer perceptron classifier를 쉽게 훈련시킬 수 있다. 그러나 point segmentation에는 local 및 global knowledge의 조합이 필요하다.
우리는 단순하지만 매우 효과적인 방법으로 이것을 달성할 수 있다.
Our solution can be seen in Fig 2 (Segmentation Network).
After computing the global point cloud feature vector, we feed it back to per point features by concatenating the global feature with each of the point features.
Then we extract new per point features based on the combined point features - this time the per point feature is aware of both the local and global information.
우리의 solution은 Fig 2(Segmentation Network)에서 확인할 수 있다.
global point cloud feature vector를 계산한 후, global feature을 각 point features과 concatenate하여 point features에 다시 공급한다.
그런 다음 결합된 point features를 기반으로 새로운 per point features를 추출한다 - 이번에는 per point features가 local 및 global information를 모두 인식합니다.
With this modification our network is able to predict per point quantities that rely on both local geometry and global semantics.
For example we can accurately predict per-point normals (fig in supplementary), validating that the network is able to summarize information from the point’s local neighborhood.
In experiment session, we also show that our model can achieve state-of-the-art performance on shape part segmentation and scene segmentation.
이 수정으로, 우리 network는 local geometry과 global semantics 모두에 의존하는 per point quantities을 예측할 수 있다.
예를 들어, 우리는 per-point normals(정규분포)를 정확하게 예측할 수 있으며, network가 point의 local neighborhood에서 정보를 요약할 수 있는지 검증할 수 있다.
실험 세션에서, 우리는 또한 우리의 model이 shape part segmentation과 scene segmentation에서 최신 성능을 달성할 수 있다는 것을 보여준다.
Joint Alignment Network
The semantic labeling of a point cloud has to be invariant if the point cloud undergoes certain geometric transformations, such as rigid transformation.
We therefore expect that the learnt representation by our point set is invariant to these transformations.
point cloud의 semantic labeling은 point cloud가 rigid transformation과 같은 특정 geometric transformations을 겪는 경우 invariant해야 한다.
따라서 point set에 의해 학습된 representation은 이러한 변환에 invariant할 것으로 예상한다.
A natural solution is to align all input set to a canonical space before feature extraction.
Jaderberg et al. [9] introduces the idea of spatial transformer to align 2D images through sampling and interpolation, achieved by a specifically tailored layer implemented on GPU.
natural solution은 feature를 추출하기 전에 모든 input set를 canonical space에 정렬하는 것입니다.
Jaderberg 등 [9]은 GPU에 구현된 특정 tailored layer에 의해 달성된 sampling 및 interpolation을 통해 2D images를 정렬하는 spatial transformer의 idea를 소개한다.
Our input form of point clouds allows us to achieve this goal in a much simpler way compared with [9].
We do not need to invent any new layers and no alias is introduced as in the image case.
We predict an affine transformation matrix by a mini-network (T-net in Fig 2) and directly apply this transformation to the coordinates of input points.
point clouds의 input form을 통해 [9]와 비교하여 훨씬 더 간단한 방법으로 이 목표를 달성할 수 있다.
우리는 새로운 layers를 발명할 필요가 없으며 image case에서와 같이 alias가 도입되지 않는다.
mini-network (T-net in Fig 2)에 의한 affine transformation matrix를 예측하고 이 변환을 input points의 좌표에 직접 적용한다.
The mininetwork itself resembles the big network and is composed by basic modules of point independent feature extraction, max pooling and fully connected layers.
More details about the T-net are in the supplementary.
mininetwork 자체는 big network와 유사하며 point independent feature extraction, max pooling 및 fully connected layers의 기본 모듈로 구성된다. T-net에 대한 자세한 내용은 부록에 나와 있습니다.
This idea can be further extended to the alignment of feature space, as well.
We can insert another alignment network on point features and predict a feature transformation matrix to align features from different input point clouds.
이 idea는 feature space의 alignment로도 확장될 수 있다.
point features에 다른 alignment network를 삽입하고 feature transformation matrix을 예측하여 서로 input point clouds의 features을 정렬할 수 있다.
However, transformation matrix in the feature space has much higher dimension than the spatial transform matrix, which greatly increases the difficulty of optimization.
We therefore add a regularization term to our softmax training loss.
그러나, feature space의 transformation matrix은 spatial transform matrix보다 훨씬 높은 차원을 가지므로 optimization의 어려움이 크게 증가한다.
따라서 softmax training loss에 regularization term을 추가한다.
We constrain the feature transformation matrix to be close to orthogonal matrix: \[L_reg = ||I - AA^T||^2_F, \qquad \qquad \qquad (1)\]
where \(A\) is the feature alignment matrix predicted by a mini-network.
여기서 \(A\)는 mini-network에 의해 예측되는 feature alignment matrix이다.
An orthogonal transformation will not lose information in the input, thus is desired.
We find that by adding the regularization term, the optimization becomes more stable and our model achieves better performance.
orthogonal transformation은 input의 information을 lose하지 않으므로, 필요하다.
regularization term을 추가하면 optimization가 더 안정화되고 model이 더 나은 성능을 달성한다는 것을 알게 된다.
4.3. Theoretical Analysis
Universal approximation
We first show the universal approximation ability of our neural network to continuous set functions.
By the continuity of set functions, intuitively, a small perturbation to the input point set should not greatly change the function values, such as classification or segmentation scores.
Formally, let \(\mathcal{X} = \{S:S \subseteq [0,1]^m \} \; and \; \|S\| = n, f : \mathcal{X} \rightarrow \mathbb{R}\)
is a continuous set function on \(\mathcal{X}\) w.r.t to
Hausdorff distance \(d_H(., .)\), i.e., \(\forall\epsilon > 0, \exists\delta > 0,\) for any \(S,S' \in \mathcal{X}, if d_H(S,S') < \delta, then \|f(S) - f'(S)\| < \epsilon\).
Our theorem says that f can be arbitrarily approximated by our network given enough neurons at the max pooling layer, i.e., K in (1) is sufficiently large.
Theorem 1. \(f : \mathcal{X} -> \mathbb{R}\) is a continuous set function w.r.t Hausdorff distance \(d_H(.,r). \forall\epsilon > 0, \exists\) a continuous function h and a symmetric function \(g(x_1, ..., x_n) = \gamma\) MAX, such that for any \(S \in X\), \[|f(S) - \gamma (MAX_{x_i\in S}\{h(x_i)\})| < \epsilon\]
where \(x_1, ... ,x_n\) is the full list of elements in \(S\) ordered arbitrarily, \(\gamma\) is a continuous function, and MAX is a vector max operator that takes n vectors as input and returns a new vector of the element-wise maximum.
The proof to this theorem can be found in our supplementary material.
The key idea is that in the worst case the network can learn to convert a point cloud into a volumetric representation, by partitioning the space into equal-sized voxels.
In practice, however, the network learns a much smarter strategy to probe the space, as we shall see in point function visualizations.
Bottleneck dimension and stability
Theoretically and experimentally we find that the expressiveness of our network is strongly affected by the dimension of the max pooling layer, i.e., \(K\) in (1).
Here we provide an analysis, which also reveals properties related to the stability of our model.
We define \(u = MAX_{x_i \in S}\{h(x_i)\}\) to be the sub-network of \(f\) which maps a point set in \([0,1]^m\) to K-dimensional vector.
The following theorem tells us that small corruptions or extra noise points in the input set are not likely to change the output of our network:
Theorem 2. \(Suppose\; u : \mathcal{X} -> \mathbb{R}^K such\, that \; u = MAX_{x_i \in S}\{h(x_i)\} \; and \; f = \gamma \circ u.\) Then,
(a) \(\forall S,\exists \mathcal{C}_S, \mathcal{N}_S \subseteq \mathcal{X}, f(T) = f(S) \; if \; \mathcal{C}_S \subseteq T \subseteq \mathcal{N}_S;\)
(b) \(\|\mathcal{C}_S\| \leq K\)
We explain the implications of the theorem.
(a) says that \(f(S)\) is unchanged up to the input corruption if all points in \(\mathcal{C}_S\) are preserved; it is also unchanged with extra noise points up to \(\mathcal{N}_S\).
(b) says that \(\mathcal{C}_S\) only contains a bounded number of points, determined by \(K\) in (1).
In other words, \(f(S)\) is in fact totally determined by a finite subset \(\mathcal{C}_S \subseteq S\) of less or equal to \(K\) elements.
We therefore call \(\mathcal{C}_S\) the critical point set of \(S\) and \(K\) the bottleneck dimension of \(f\).
Combined with the continuity of h, this explains the robustness of our model w.r.t point perturbation, corruption and extra noise points.
The robustness is gained in analogy to the sparsity principle in machine learning models.
Intuitively, our network learns to summarize a shape by a sparse set of key points.
In experiment section we see that the key points form the skeleton of an object.
5. Experiment
Experiments are divided into four parts. First, we show PointNets can be applied to multiple 3D recognition tasks (Sec 5.1).
Second, we provide detailed experiments to validate our network design (Sec 5.2). At last we visualize what the network learns (Sec 5.3) and analyze time and space complexity (Sec 5.4).
5.1. Applications
In this section we show how our network can be trained to perform 3D object classification, object part segmentation and semantic scene segmentation 1. Even though we are working on a brand new data representation (point sets), we are able to achieve comparable or even better performance on benchmarks for several tasks.
3D Object Classification
Our network learns global point cloud feature that can be used for object classification.
We evaluate our model on the ModelNet40 [28] shape classification benchmark.
There are 12,311 CAD models from 40 man-made object categories, split into 9,843 for training and 2,468 for testing.
While previous methods focus on volumetric and mult-view image representations, we are the first to directly work on raw point cloud.
We uniformly sample 1024 points on mesh faces according to face area and normalize them into a unit sphere.
During training we augment the point cloud on-the-fly by randomly rotating the object along the up-axis and jitter the position of each points by a Gaussian noise with zero mean and 0.02 standard deviation.
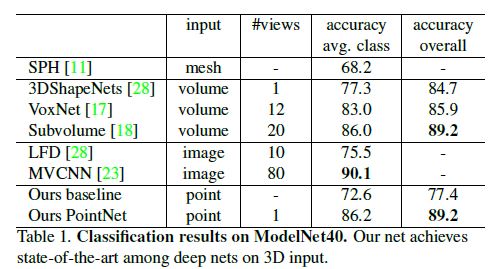
In Table 1, we compare our model with previous works as well as our baseline using MLP on traditional features extracted from point cloud (point density, D2, shape contour etc.).
Our model achieved state-of-the-art performance among methods based on 3D input (volumetric and point cloud).
With only fully connected layers and max pooling, our net gains a strong lead in inference speed and can be easily parallelized in CPU as well.
There is still a small gap between our method and multi-view based method (MVCNN [23]), which we think is due to the loss of fine geometry details that can be captured by rendered images.
3D Object Part Segmentation
Part segmentation is a challenging fine-grained 3D recognition task.
Given a 3D scan or a mesh model, the task is to assign part category label (e.g. chair leg, cup handle) to each point or face.
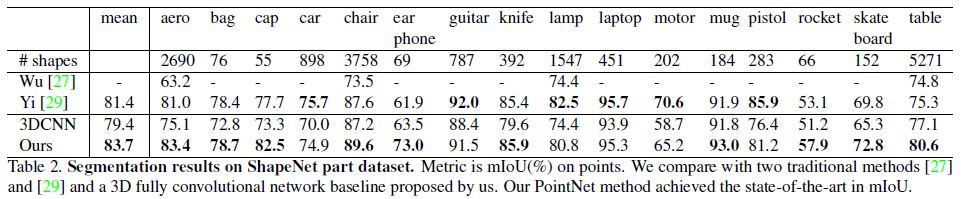
We evaluate on ShapeNet part data set from [29], which contains 16,881 shapes from 16 categories, annotated with 50 parts in total.
Most object categories are labeled with two to five parts. Ground truth annotations are labeled on sampled points on the shapes.
We formulate part segmentation as a per-point classification problem.
Evaluation metric is mIoU on points.
For each shape S of category C, to calculate the shape’s mIoU: For each part type in category C, compute IoU between groundtruth and prediction.
If the union of groundtruth and prediction points is empty, then count part IoU as 1.
Then we average IoUs for all part types in category C to get mIoU for that shape. To calculate mIoU for the category, we take average of mIoUs for all shapes in that category.
In this section, we compare our segmentation version PointNet (a modified version of Fig 2, Segmentation Network) with two traditional methods [27] and [29] that both take advantage of point-wise geometry features and correspondences between shapes, as well as our own 3D CNN baseline.
See supplementary for the detailed modifications and network architecture for the 3D CNN.
In Table 2, we report per-category and mean IoU(%) scores.
We observe a 2.3% mean IoU improvement and our net beats the baseline methods in most categories.
We also perform experiments on simulated Kinect scans to test the robustness of these methods.
For every CAD model in the ShapeNet part data set, we use Blensor Kinect Simulator [7] to generate incomplete point clouds from six random viewpoints.
We train our PointNet on the complete shapes and partial scans with the same network architecture and training setting.
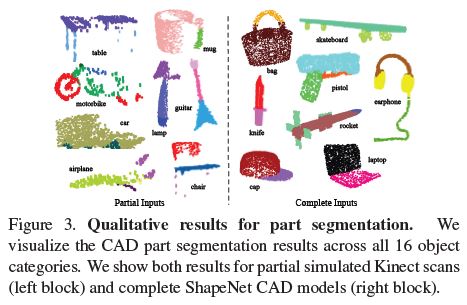
Results show that we lose only 5.3% mean IoU. In Fig 3, we present qualitative results on both complete and partial data. One can see that though partial data is fairly challenging, our predictions are reasonable.
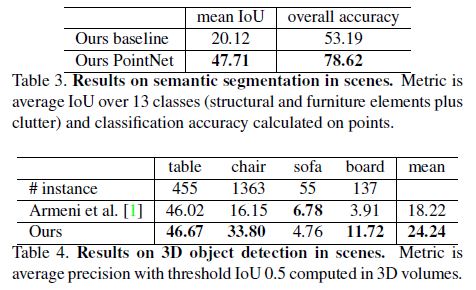
Semantic Segmentation in Scenes
Our network on part segmentation can be easily extended to semantic scene segmentation, where point labels become semantic object classes instead of object part labels.
We experiment on the Stanford 3D semantic parsing data set [1].
The dataset contains 3D scans from Matterport scanners in 6 areas including 271 rooms.
Each point in the scan is annotated with one of the semantic labels from 13 categories (chair, table, floor, wall etc. plus clutter).
To prepare training data, we firstly split points by room, and then sample rooms into blocks with area 1m by 1m.
We train our segmentation version of PointNet to predict per point class in each block.
Each point is represented by a 9-dim vector of XYZ, RGB and normalized location as to the room (from 0 to 1).
At training time, we randomly sample 4096 points in each block on-the-fly.
At test time, we test on all the points. We follow the same protocol as [1] to use k-fold strategy for train and test.
We compare our method with a baseline using handcrafted point features.
The baseline extracts the same 9- dim local features and three additional ones: local point density, local curvature and normal.
We use standard MLP as the classifier. Results are shown in Table 3, where our PointNet method significantly outperforms the baseline method.
In Fig 4, we show qualitative segmentation results.
Our network is able to output smooth predictions and is robust to missing points and occlusions.
Based on the semantic segmentation output from our network, we further build a 3D object detection system using connected component for object proposal (see supplementary for details).
We compare with previous stateof-the-art method in Table 4.
The previous method is based on a sliding shape method (with CRF post processing) with SVMs trained on local geometric features and global room context feature in voxel grids.
Our method outperforms it by a large margin on the furniture categories reported.
5.2. Architecture Design Analysis
In this section we validate our design choices by control experiments.
We also show the effects of our network’s hyperparameters.
Comparison with Alternative Order-invariant Methods As mentioned in Sec 4.2, there are at least three options for consuming unordered set inputs.
We use the ModelNet40 shape classification problem as a test bed for comparisons of those options, the following two control experiment will also use this task.
The baselines (illustrated in Fig 5) we compared with include multi-layer perceptron on unsorted and sorted points as n x 3 arrays, RNN model that considers input point as a sequence, and a model based on symmetry functions.
The symmetry operation we experimented include max pooling, average pooling and an attention based weighted sum.
The attention method is similar to that in [25], where a scalar score is predicted from each point feature, then the score is normalized across points by computing a softmax.
The weighted sum is then computed on the normalized scores and the point features. As shown in Fig 5, maxpooling operation achieves the best performance by a large winning margin, which validates our choice.
Effectiveness of Input and Feature Transformations
In Table 5 we demonstrate the positive effects of our input and feature transformations (for alignment).
It’s interesting to see that the most basic architecture already achieves quite reasonable results.
Using input transformation gives a 0.8% performance boost.
The regularization loss is necessary for the higher dimension transform to work.
By combining both transformations and the regularization term, we achieve the best performance.
Robustness Test We show our PointNet, while simple and effective, is robust to various kinds of input corruptions.
We use the same architecture as in Fig 5’s max pooling network.
Input points are normalized into a unit sphere.
Results are in Fig 6.
As to missing points, when there are 50% points missing, the accuracy only drops by 2.4% and 3.8% w.r.t. furthest and random input sampling.
Our net is also robust to outlier points, if it has seen those during training.
We evaluate two models: one trained on points with (x, y, z) coordinates; the other on (x, y, z) plus point density.
The net has more than 80% accuracy even when 20% of the points are outliers.
Fig 6 right shows the net is robust to point perturbations.
5.3. Visualizing PointNet
In Fig 7, we visualize critical point sets \(\mathcal{C}_S\) and upperbound shapes \(\mathcal{N}_S\) (as discussed in Thm 2) for some sample shapes S.
The point sets between the two shapes will give exactly the same global shape feature \(f(S)\).
We can see clearly from Fig 7 that the critical point sets \(\mathcal{C}_S\), those contributed to the max pooled feature, summarizes the skeleton of the shape.
The upper-bound shapes NS illustrates the largest possible point cloud that give the same global shape feature \(f(S)\) as the input point cloud \(S\).
\(\mathcal{C}_S\) and \(\mathcal{N}_S\) reflect the robustness of PointNet, meaning that losing some non-critical points does not change the global shape signature \(f(S)\) at all.
The \(\mathcal{N}_S\) is constructed by forwarding all the points in a edge-length-2 cube through the network and select points p whose point function values \((h_1(p), h_2(p), ... , h_K(p))\) are no larger than the global shape descriptor.
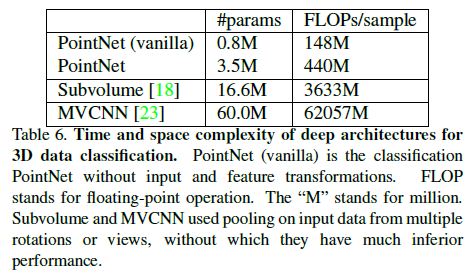
5.4. Time and Space Complexity Analysis
Table 6 summarizes space (number of parameters in the network) and time (floating-point operations/sample) complexity of our classification PointNet.
We also compare PointNet to a representative set of volumetric and multiview based architectures in previous works.
While MVCNN [23] and Subvolume (3D CNN) [18] achieve high performance, PointNet is orders more efficient in computational cost (measured in FLOPs/sample: 141x and 8x more efficient, respectively).
Besides, PointNet is much more space efficient than MVCNN in terms of #param in the network (17x less parameters). Moreover, PointNet is much more scalable – it’s space and time complexity is O(N) – linear in the number of input points.
However, since convolution dominates computing time, multi-view method’s time complexity grows squarely on image resolution and volumetric convolution based method grows cubically with the volume size.
Empirically, PointNet is able to process more than one million points per second for point cloud classification (around 1K objects/second) or semantic segmentation (around 2 rooms/second) with a 1080X GPU on Tensor-Flow, showing great potential for real-time applications.
6. Conclusion
In this work, we propose a novel deep neural network PointNet that directly consumes point cloud.
Our network provides a unified approach to a number of 3D recognition tasks including object classification, part segmentation and semantic segmentation, while obtaining on par or better results than state of the arts on standard benchmarks.
We also provide theoretical analysis and visualizations towards understanding of our network.
Acknowledgement. The authors gratefully acknowledge the support of a Samsung GRO grant, ONR MURI N00014-13-1-0341 grant, NSF grant IIS-1528025, a Google Focused Research Award, a gift from the Adobe corporation and hardware donations by NVIDIA.