PointNet++
: Deep Hierarchical Feature Learning on Point Sets in a Metric Space
NIPS 2017 paper
Abstract
Few prior works study deep learning on point sets.
PointNet [20] is a pioneer in this direction.
However, by design PointNet does not capture local structures induced by the metric space points live in, limiting its ability to recognize fine-grained patterns and generalizability to complex scenes.
point sets에 대한 deep learning을 연구하는 선행 연구는 거의 없다.
PointNet[20]은 이 방향의 선구자이다.
그러나 설계상 PointNet은 metric space points에 의해 유도된 local structures를 캡처하지 않으므로, fine-grained patterns과 generalizability를 complex scenes으로 인식하는 기능이 제한된다.
In this work, we introduce a hierarchical neural network that applies PointNet recursively on a nested partitioning of the input point set.
By exploiting metric space distances, our network is able to learn local features with increasing contextual scales.
With further observation that point sets are usually sampled with varying densities, which results in greatly decreased performance for networks trained on uniform densities, we propose novel set learning layers to adaptively combine features from multiple scales.
본 연구에서는 input point set의 중첩된 분할(nested partitioning)에 PointNet을 재귀적으로 적용하는 계층적 신경망(hierarchical neural network)을 소개한다.
metric space distances를 이용하여, 우리의 네트워크는 상황별 스케일(contextual scales)을 증가시키는 local features을 배울 수 있다.
point sets가 일반적으로 다양한 밀도(varying densities)로 샘플링되어 균일한 밀도(uniform densities)로 훈련된 networks의 성능이 크게 저하된다는 추가 관찰을 통해, 우리는 multiple scales의 features을 적응적으로 결합하기 위한 novel set learning layers을 제안한다.
Experiments show that our network called PointNet++ is able to learn deep point set features efficiently and robustly.
In particular, results significantly better than state-of-the-art have been obtained on challenging benchmarks of 3D point clouds.
1 Introduction
A particularly important type of geometric point set is point cloud captured by 3D scanners, e.g., from appropriately equipped autonomous vehicles.
우리는 Euclidean space의 points 집합인 geometric point sets을 분석하는 데 관심이 있다.
특히 중요한 유형의 geometric point set는 3D 스캐너(예: 적절한 장비를 갖춘 자율 주행 차량)에 의해 포착된 point cloud이다.
.
For example, the density and other attributes of points may not be uniform across different locations — in 3D scanning the density variability can come from perspective effects, radial density variations, motion, etc.
집합으로서, 그러한 데이터는 구성원의 permutations에 invariant해야 한다.
또한 distance metric은 다른 properties을 나타낼 수 있는 local neighborhoods을 정의한다.
예를 들어, points의 밀도 및 기타 속성은 서로 다른 위치에 걸쳐 균일하지 않을 수 있다.
3D 스캐닝에서 density variability은 원근 효과(perspective effects), 방사형 밀도 변화(radial density variations), motion 등에서 발생할 수 있다.
Few prior works study deep learning on point sets.
PointNet [20] is a pioneering effort that directly processes point sets.
By its design, PointNet does not capture local structure induced by the metric.
point sets에 대한 deep learning을 연구하는 선행 연구는 거의 없다.
PointNet[20]은 point sets를 직접 처리하는 선구적인 노력이다. PointNet의 기본 아이디어는 각 point의 공간 인코딩을 학습한 다음 모든 개별 point features을 global point cloud signature에 통합하는 것이다. 설계상 PointNet은 metric에 의해 유도된 local structure를 캡처하지 않는다.
A CNN takes data defined on regular grids as the input and is able to progressively capture features at increasingly larger scales along a multi-resolution hierarchy.
At lower levels neurons have smaller receptive fields whereas at higher levels they have larger receptive fields.
The ability to abstract local patterns along the hierarchy allows better generalizability to unseen cases.
그러나 local structure를 활용하는 것이 convolutional architectures의 성공에 중요한 것으로 입증되었다. CNN은 정규 그리드에 정의된 데이터를 입력으로 사용하고 multi-resolution hierarchy을 따라 점점 더 큰 scales로 features을 점진적으로 캡처할 수 있다. lower levels에서 neurons은 더 작은 수용 영역(receptive fields)을 가지는 반면 higher levels에서 더 큰 수용 영역을 가진다. hierarchy에 따라 local patterns을 추상화(abstract)하는 기능을 통해 보이지 않는 사례에 대한 generalizability를 개선할 수 있다.
The general idea of PointNet++ is simple.
metric space에서 샘플링된 points 집합을 계층적 방식(hierarchical fashion)으로 처리하기 위해 PointNet++라는 이름의 계층적 신경망을 도입한다.
PointNet++의 일반적인 아이디어는 간단하다.
먼저 기본 공간(underlying space)의 distance metric에 따라 points 집합을 overlapping하는 local regions으로 분할한다.
CNN과 유사하게, 우리는 small neighborhoods에서 fine geometric structures를 캡처하는 local features을 추출한다; 이러한 local features은 더 큰 단위로 그룹화되어 더 높은 수준의 features을 생성하기 위해 처리된다.
이 프로세스는 전체 point set의 특징을 얻을 때까지 반복됩니다.
The two issues are correlated because the partitioning of the point set has to produce common structures across partitions, so that weights of local feature learners can be shared, as in the convolutional setting.
PointNet++의 설계는 두 가지 문제를 해결해야 한다 : point set의 partitioning을 생성하는 방법과 local feature learner를 통해 points 집합 또는 local features을 추상화하는 방법.
두 문제는 point set의 분할이 partitions 간에 공통 구조를 생성하여, convolutional setting에서처럼 local feature learners의 weights를 공유할 수 있기 때문에 상관관계가 있다.
We choose our local feature learner to be PointNet.
As demonstrated in that work,
In addition, this architecture is robust to input data corruption.
As a basic building block, PointNet abstracts sets of local points or features into higher level representations.
local feature learner를 PointNet으로 선택합니다. 그 연구에서 입증되었듯이, PointNet은 의미론적 특징 추출(semantic feature extraction)을 위해 unordered set of points을 처리하는 효과적인 아키텍처이다. 또한 이 아키텍처는 입력 데이터 손상에도 robust하다.
기본 구성 block으로서, PointNet은 local points 또는 features 집합을 더 높은 수준의 representations으로 추상화한다. this view에서, PointNet++는 입력 세트의 중첩된 분할(nested partitioning)에 반복적으로 PointNet을 적용합니다.
One issue that still remains is how to generate overlapping partitioning of a point set.
Each partition is defined as a neighborhood ball in the underlying Euclidean space, whose parameters include centroid location and scale.
여전히 남아 있는 문제 중 하나는 point set의 중첩 분할(overlapping partitioning)을 생성하는 방법이다.
각 partition은 centroid location 와 scale를 포함하는 기본 유클리드 공간(underlying Euclidean space)에서 neighborhood ball으로 정의된다.
To evenly cover the whole set, the centroids are selected among input point set by a farthest point sampling (FPS) algorithm.
Compared with volumetric CNNs that scan the space with fixed strides, our local receptive fields are dependent on both the input data and the metric, and thus more efficient and effective.
전체 set를 균일하게 커버하기 위해, 가장 먼 포인트 샘플링(FPS:farthest point sampling) algorithm에 의해 설정된 input point set 중에서 centroids를 선택합니다.
고정된 stride로 공간을 스캔하는 volumetric CNNs과 비교하여, 우리의 local receptive fields는 input data와 metric 모두에 의존하며, 따라서 더 효율적이고 효과적이다
Deciding the appropriate scale of local neighborhood balls, however, is a more challenging yet intriguing problem, due to the entanglement of feature scale and non-uniformity of input point set.
We assume that the input point set may have variable density at different areas, which is quite common in real data such as Structure Sensor scanning [18] (see Fig. 1).
그러나 local neighborhood balls의 적절한 scale을 결정하는 것은 feature scale의 entanglement과 input point set의 불균일성으로 인해 더 어렵지만 흥미로운 문제이다. 우리는 input point set가 Structure Sensor scanning [18]과 같은 실제 데이터에서 상당히 흔한 서로 다른 영역에서 variable density를 가질 수 있다고 가정한다 (그림 1 참조).
Our input point set is thus very different from CNN inputs which can be viewed as data defined on regular grids with uniform constant density.
In CNNs, the counterpart to local partition scale is the size of kernels.
[25] shows that using smaller kernels helps to improve the ability of CNNs.
Our experiments on point set data, however, give counter evidence to this rule.
따라서 우리의 input point set는 일정한 밀도가 균일한 정규 그리드에서 정의된 데이터로 볼 수 있는 CNN 입력과는 매우 다르다.
CNN에서 local partition scale의 상대는 커널 크기이다.
[25]는 더 작은 커널을 사용하는 것이 CNN의 능력을 향상시키는 데 도움이 된다는 것을 보여준다.
그러나 점 집합 데이터에 대한 우리의 실험은 이 규칙에 대한 반대 증거를 제공한다.
Small neighborhood은 sampling 부족으로 인해 너무 적은 points으로 구성될 수 있으며, 이는 PointNet이 패턴을 강력하게 캡처하는 데 충분하지 않을 수 있다.
A significant contribution of our paper is that PointNet++ leverages neighborhoods at multiple scales to achieve both robustness and detail capture.
Assisted with random input dropout during training, the network learns to adaptively weight patterns detected at different scales and combine multi-scale features according to the input data.
Experiments show that our PointNet++ is able to process point sets efficiently and robustly.
In particular, results that are significantly better than state-of-the-art have been obtained on challenging benchmarks of 3D point clouds.
본 논문의 중요한 기여는 PointNet++가 neighborhoods을 multiple scales로 활용하여 robustness과 detail capture를 모두 달성한다는 것이다.
training 중 random input dropout을 지원받아, network는 다양한 규모로 감지된 패턴에 적응적으로 weight를 부여하고 입력 데이터에 따라 multi-scale features을 결합하는 방법을 배운다.
실험에 따르면 우리의 PointNet++는 point sets를 효율적이고 강력하게 처리할 수 있다.
특히, 3D point clouds의 까다로운 benchmarks에서 최신논문보다 훨씬 나은 결과를 얻었다.
2 Problem Statement
Suppose that \(\mathcal{X} = (M,d)\) is a discrete metric space whose metric is inherited from a Euclidean space \(\mathbb{R}^n\), where \(M \subseteq \mathbb{R}^n\) is the set of points and \(d\) is the distance metric.
In addition, the density of \(M\) in the ambient Euclidean space may not be uniform everywhere.
We are interested in learning set functions \(f\) that take such \(\mathcal{X}\) as the input (along with additional features for each point) and produce information of semantic interest regrading \(\mathcal{X}\).
In practice, such \(f\) can be classification function that assigns a label to \(\mathcal{X}\) or a segmentation function that assigns a per point label to each member of \(M\).
ambient Euclidean space : 수학에서, 환경 공간(영어: ambient space)은 공간을 둘러싸는 공간이다.
3 Method
Our work can be viewed as an extension of PointNet [20] with added hierarchical structure.
We first review PointNet (Sec. 3.1) and then introduce a basic extension of PointNet with hierarchical structure (Sec. 3.2).
Finally, we propose our PointNet++ that is able to robustly learn features even in non-uniformly sampled point sets (Sec. 3.3).
우리의 작업은 hierarchical structure가 추가된 PointNet [20]의 확장으로 볼 수 있다.
먼저 PointNet(Sec. 3.1)을 review한 다음 hierarchical structure를 가진 PointNet의 기본 확장을 소개한다.(Sec. 3.2)
마지막으로, 불균일하게 샘플링된 point sets에서도 기능을 강력하게 학습할 수 있는 PointNet++를 제안한다(Sec. 3.3).
3.1 Review of PointNet [20]: A Universal Continuous Set Function Approximator
Given an unordered point set \(\{x_1, x_2, ...,x_n\} \; with \; x_i \in \mathbb{R}^d\), one can define a set function \(f : \mathbb{X} \rightarrow \mathbb{R}\) that maps a set of points to a vector: \[f({x_1, ... , x_n}) \approx \gamma(MAX_{i=1,..,n}\{h(x_i)\}), \qquad \qquad \qquad (1)\]
where \(\gamma\) and \(h\) are usually multi-layer perceptron (MLP) networks.
The set function \(f\) in Eq. 1 is invariant to input point permutations and can arbitrarily approximate any continuous set function [20].
Note that the response of \(h\) can be interpreted as the spatial encoding of a point (see [20] for details).
PointNet achieved impressive performance on a few benchmarks.
However, it lacks the ability to capture local context at different scales.
We will introduce a hierarchical feature learning framework in the next section to resolve the limitation.
PointNet은 몇 가지 benchmarks에서 인상적인 성능을 달성했다.
그러나 다른 scales로 local context를 캡처할 수 있는 기능이 부족하다.
우리는 한계를 해결하기 위해 다음 절에 hierarchical feature learning framework를 도입할 것이다.
3.2 Hierarchical Point Set Feature Learning
While
PointNet은 single max pooling operation을 사용하여 전체 point set를 집계하지만, 우리의 새로운 아키텍처는 포인트의 hierarchical grouping을 구축하고 hierarchy을 따라 점점 더 큰 local regions을 추상화한다.
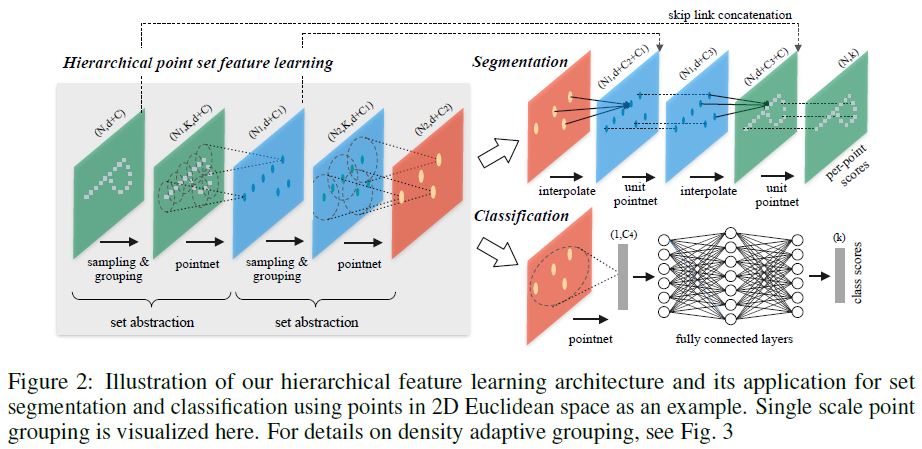
Our hierarchical structure is composed by a number of set abstraction levels (Fig. 2).
우리의 계층 구조는 많은 집합 추상화 수준으로 구성된다(그림 2).
각 수준에서 points 집합이 처리되고 추상화되어 더 적은 수의 요소로 새 집합을 생성한다.
The set abstraction level is made of three key layers:
Sampling layer selects a set of points from input points, which defines the centroids of local regions.
Grouping layer then constructs local region sets by finding “neighboring” points around the centroids.
PointNet layer uses a mini-PointNet to encode local region patterns into feature vectors.
Sampling layer는 input points에서 points 집합을 선택하여 local regions의 중심을 정의
Grouping layer 그런 다음 중심 주위에 “neighboring” points을 찾아 local region sets을 구성
PointNet 레이어는 mini-PointNet을 사용하여 local region patterns을 feature vectors로 인코딩
A set abstraction level takes an \(N \times (d + C)\) matrix as input that is from \(N\) points with \(d\)-dim coordinates and \(C\)-dim point feature.
It outputs an \(N' \times (d + C')\) matrix of \(N'\) subsampled points with \(d\)-dim coordinates and new \(C'\)-dim feature vectors summarizing local context.
We introduce the layers of a set abstraction level in the following paragraphs.
Sampling layer.
Given input points \({x_1, x_2, ..., x_n}\), we use iterative farthest point sampling (FPS) to choose a subset of points \(\{x_{i_1}, x_{i_2}, ...,x_{i_m}\}\), such that \(x_{i_j}\) is the most distant point (in metric distance) from the set \(\{x_{i_1}, x_{i_2}, ... , x_{i_{j-1}}\}\) with regard to the rest points.
Compared with random sampling, it has better coverage of the entire point set given the same number of centroids.
In contrast to CNNs that scan the vector space agnostic of data distribution, our sampling strategy generates receptive fields in a data dependent manner.
vector space agnostic of data distribution
Grouping layer.
The input to this layer is a point set of size \(N \times (d + C)\) and the coordinates of a set of centroids of size \(N' \times d\).
The output are groups of point sets of size \(N' \times K \times (d + C)\), where each group corresponds to a local region and \(K\) is the number of points in the neighborhood of centroid points. Note that \(K\) varies across groups but the succeeding PointNet layer is able to convert flexible number of points into a fixed length local region feature vector.
In convolutional neural networks, a local region of a pixel consists of pixels with array indices within certain Manhattan distance (kernel size) of the pixel.
In a point set sampled from a metric space, the neighborhood of a point is defined by metric distance.
Ball query finds all points that are within a radius to the query point (an upper limit of \(K\) is set in implementation).
An alternative range query is \(K\) nearest neighbor (kNN) search which finds a fixed number of neighboring points.
Compared with kNN, ball query’s local neighborhood guarantees a fixed region scale thus making local region feature more generalizable across space, which is preferred for tasks requiring local pattern recognition (e.g. semantic point labeling).
PointNet layer.
In this layer, the input are \(N'\) local regions of points with data size \(N' \times K \times (d+C)\).
Each local region in the output is abstracted by its centroid and local feature that encodes the centroid’s neighborhood. Output data size is \(N' \times (d + C')\).
The coordinates of points in a local region are firstly translated into a local frame relative to the centroid point: \(x^{(j)}_i = x^{(j)}_i − \hat{x}^{(j)} \; for \; i = 1, 2, ...,K \; and \; j = 1, 2, ...,d\) where \(\hat{x}\) is the coordinate of the centroid.
We use PointNet [20] as described in Sec. 3.1 as the basic building block for local pattern learning.
By using relative coordinates together with point features we can capture point-to-point relations in the local region.
3.3 Robust Feature Learning under Non-Uniform Sampling Density
Such non-uniformity introduces a significant challenge for point set feature learning.
Features learned in dense data may not generalize to sparsely sampled regions.
Consequently, models trained for sparse point cloud may not recognize fine-grained local structures.
앞에서 설명한 것처럼 point set은 서로 다른 영역에서 균일하지 않은 밀도를 갖는 것이 일반적입니다.
이러한 불균일성은 point set feature learning에 중요한 도전을 도입한다. dense된 데이터에서 학습된 Features은 sparse하게 샘플링된 regions으로 generalize되지 않을 수 있다.
결과적으로, sparse point cloud에 대해 훈련된 model은 fine-grained local structures를 인식하지 못할 수 있다.
However, such close inspect is prohibited at low density areas because local patterns may be corrupted by the sampling deficiency.
We call our hierarchical network with density adaptive PointNet layers as PointNet++.
이상적으로, 우리는 가능한 한 point set를 면밀히 검사하여 densely하게 샘플링된 regions에서 finest details를 캡처하기를 원한다. 그러나 local patterns이 sampling 부족에 의해 손상될 수 있으므로 low density areas에서 이러한 close inspect가 금지된다. 이 경우, 우리는 greater vicinity에서 larger scale patterns을 찾아야 합니다. 이 목표를 달성하기 위해 input sampling density가 변경될 때 서로 다른 scales의 regions에서 features을 결합하는 방법을 배우는 density adaptive PointNet layers (Fig. 3)를 제안한다. density adaptive PointNet layers을 가진 hierarchical network를 PointNet++ 이라고 부른다.
Previously in Sec. 3.2, each abstraction level contains grouping and feature extraction of a single scale.
.
In terms of grouping local regions and combining features from different scales, we propose two types of density adaptive layers as listed below.
이전 Sec. 3.2에서 각 추상화 level은 single scale의 그룹화 및 특징 추출을 포함한다. PointNet++에서 각 추상화 level은 local patterns의 여러 scales를 추출하고 local point density에 따라 지능적으로 결합한다. local regions을 그룹화하고 서로 다른 scales의 features을 결합하는 측면에서, 우리는 아래 나열된 두 가지 유형의 density adaptive layers을 제안한다.
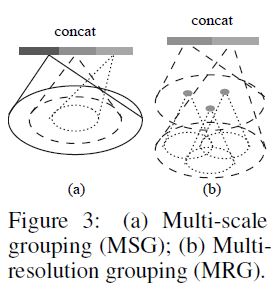
Multi-scale grouping (MSG).
As shown in Fig. 3 (a), a simple but effective way to capture multiscale patterns is to apply grouping layers with different scales followed by according PointNets to extract features of each scale.
Features at different scales are concatenated to form a multi-scale feature.
Fig. 3 (a)에서 보듯이, multiscale patterns을 캡처하는 간단하지만 효과적인 방법은 서로 다른 scales의 Grouping layers를 적용한 후 PointNets에 따라 각 scale의 features을 추출하는 것이다. 서로 다른 scales의 Features가 연결되어 multi-scale feature를 형성한다.
We train the network to learn an optimized strategy to combine the multi-scale features.
This is done by randomly dropping out input points with a randomized probability for each instance, which we call random input dropout.
Specifically, for each training point set, we choose a dropout ratio \(\theta\) uniformly sampled from \([0, p]\) where \(p \leq 1\).
For each point, we randomly drop a point with probability \(\theta\).
In practice we set \(p = 0.95\) to avoid generating empty point sets.
In doing so we present the network with training sets of various sparsity (induced by \(\theta\)) and varying uniformity (induced by randomness in dropout).
During test, we keep all available points.
우리는 네트워크를 훈련시켜 multi-scale features을 결합하는 optimize화된 strategy을 학습한다. 이는 각 instance에 대해 randomized probability로 input points를 랜덤하게 dropout하는 방식으로 수행되며, 이를 random input dropout이라고 한다. 구체적으로, 각 training point set에 대해, 우리는 \([0, p]\)에서 균일하게 샘플링된 dropout ratio \(\theta\)를 선택한다, where \(p \leq 1\).
각 point에 대해, 우리는 probability \(\theta\)인 point을 랜덤하게 drop한다.
실제로 우리는 빈 point sets를 생성하지 않도록 \(p = 0.95\)를 설정한다.
이를 통해 우리는 다양한 sparsity (induced by \(\theta\))와 다양한 uniformity(induced by randomness in dropout)의 training sets와 함께 네트워크를 제시한다. 테스트 중에는 사용 가능한 모든 points를 유지한다.
Multi-resolution grouping (MRG).
The MSG approach above is computationally expensive since it runs local PointNet at large scale neighborhoods for every centroid point.
In particular, since the number of centroid points is usually quite large at the lowest level, the time cost is significant.
위의 MSG 접근 방식은 모든 centroid point에 대해 large scale neighborhoods에서 local PointNet을 실행하므로 계산 비용이 많이 든다.
특히 centroid points 개수는 일반적으로 lowest level에서 상당히 크기 때문에 시간 비용이 중요하다.
Here we propose an alternative approach that avoids such expensive computation but still preserves the ability to adaptively aggregate information according to the distributional properties of points.
In Fig. 3 (b), features of a region at some level \(L_i\) is a concatenation of two vectors.
One vector (left in figure) is obtained by summarizing the features at each subregion from the lower level \(L_{i−1}\) using the set abstraction level.
The other vector (right) is the feature that is obtained by directly processing all raw points in the local region using a single PointNet.
여기서 우리는 그러한 비용이 큰 계산을 피하면서 points의 distributional properties에 따라 정보를 adaptively로 집계할 수 있는 능력을 보존하는 대안적 접근법을 제안한다.
Fig. 3 (b)에서, level \(L_i\)에서의 region의 features은 두 벡터의 결합이다.
One vector는 set abstraction level을 사용하여 lower level \(L_{i−1}\)에서 각 subregion의 features을 요약함으로써 얻어진다.
The other vector는 단일 PointNet을 사용하여 local region의 모든 raw points을 직접 처리함으로써 얻을 수 있는 feature이다.
When the density of a local region is low, the first vector may be less reliable than the second vector, since the subregion in computing the first vector contains even sparser points and suffers more from sampling deficiency.
In such a case, the second vector should be weighted higher.
On the other hand, when the density of a local region is high, the first vector provides information of finer details since it possesses the ability to inspect at higher resolutions recursively in lower levels.
local region의 density가 낮을 때, first vector는 second vector보다 신뢰성이 낮을 수 있는데, first vector의 계산에서 subregion은 훨씬 더 sparser points을 포함하고 더 많은 샘플링 결핍을 겪기 때문이다. 이러한 경우, second vector는 가중치가 더 높아야 한다.
반면에, local region의 밀도가 높을 때, first vector는 lower levels에서 더 높은 resolutions에서 반복적으로 검사할 수 있는 능력을 가지고 있기 때문에 finer details 정보를 제공한다.
Compared with MSG, this method is computationally more efficient since we avoids the feature extraction in large scale neighborhoods at lowest levels.
MSG와 비교하여 이 방법은 lowest levels의 large scale neighborhoods에서 feature 추출을 피하기 때문에 계산적으로 더 효율적이다.
3.4 Point Feature Propagation for Set Segmentation
In set abstraction layer, the original point set is subsampled.
However in set segmentation task such as semantic point labeling, we want to obtain point features for all the original points.
One solution is to always sample all points as centroids in all set abstraction levels, which however results in high computation cost.
Another way is to propagate features from subsampled points to the original points.
We adopt a hierarchical propagation strategy with distance based interpolation and across level skip links (as shown in Fig. 2).
set abstraction layer에서는, original point set이 하위 샘플링된다.
그러나 semantic point labeling과 같은 set segmentation task에서, 우리는 모든 original points에 대한 point features을 얻기를 원한다.
한 가지 해결책은 set abstraction levels에서 항상 모든 points을 중심점으로 샘플링하는 것이지만, 이는 높은 계산 비용을 초래한다. 또 다른 방법은 하위 샘플링된 points의 형상을 original points으로 전파하는 것이다.
우리는 interpolation 기반 distance 및 across level skip links를 가진 hierarchical propagation strategy을 채택한다.
In a feature propagation level, we propagate point features from \(N_l \times (d+C)\) points to \(N_{l−1}\) points where \(N_{l−1}\) and \(N_l\) (with \(N_l \leq N_{l−1}\)) are point set size of input and output of set abstraction level l.
We achieve feature propagation by interpolating feature values \(f\) of \(N_l\) points at coordinates of the \(N_{l−1}\) points.
feature propagation level에서, 우리는 \(N_l \times (d+C)\) points에서 \(N_{l−1}\) points 및 \(N_l\) (with \(N_l \leq N_{l−1}\))가 input의 point set size와 set abstraction level l의 output인 \(N_{l−1}\) points로 특징을 전파한다.
\(N_{l−1}\) points의 좌표에 \(N_l\) points의 feature values \(f\)를 interpolating하여 feature propagation를 달성한다.
Among the many choices for interpolation, we use inverse distance weighted average based on \(k\) nearest neighbors (as in Eq. 2, in default we use \(p = 2, k = 3\)).
The interpolated features on \(N_{l−1}\) points are then concatenated with skip linked point features from the set abstraction level.
Then the concatenated features are passed through a “unit pointnet”, which is similar to one-by-one convolution in CNNs.
A few shared fully connected and ReLU layers are applied to update each point’s feature vector.
The process is repeated until we have propagated features to the original set of points.
interpolation을 위한 많은 선택 중에서, 우리는 \(k\) 가장 가까운 neighbors에 기초한 inverse distance weighted average을 사용한다.
그런 다음 \(N_{l−1}\) points의 interpolated features은 set abstraction level에서 skip linked point features와 concatenate된다.
그런 다음 concatenated features가 “unit pointnet”을 통해 전달되는데, 이는 CNN의 one-by-one convolution과 유사하다. A few shared fully connected and ReLU layers가 각 point의 feature vector를 업데이트하기 위해 적용된다. original points 집합으로 features을 전파할 때까지 process가 반복된다.
4 Experiments
Datasets
We evaluate on four datasets ranging from 2D objects (MNIST [11]), 3D objects (ModelNet40 [31] rigid object, SHREC15 [12] non-rigid object) to real 3D scenes (ScanNet [5]).
Object classification is evaluated by accuracy.
Semantic scene labeling is evaluated by average voxel classification accuracy following [5].
우리는 2D objects (MNIST [11]), D objects (ModelNet40 [31] rigid object, SHREC15 [12] non-rigid object)에서 real 3D scenes (ScanNet [5])에 이르는 4가지 데이터 세트에서 evaluate한다.
Object classification는 정확성에 의해 평가됩니다. Semantic scene labeling은 [5] 이후 average voxel classification accuracy로 평가된다.
We list below the experiment setting for each dataset:
- MNIST: Images of handwritten digits with 60k training and 10k testing samples.
- ModelNet40: CAD models of 40 categories (mostly man-made). We use the official split with 9,843 shapes for training and 2,468 for testing.
- SHREC15: 1200 shapes from 50 categories. Each category contains 24 shapes which are mostly organic ones with various poses such as horses, cats, etc. We use five fold cross validation to acquire classification accuracy on this dataset.
- ScanNet: 1513 scanned and reconstructed indoor scenes. We follow the experiment setting in [5] and use 1201 scenes for training, 312 scenes for test.
4.1 Point Set Classification in Euclidean Metric Space
We evaluate our network on classifying point clouds sampled from both 2D (MNIST) and 3D (ModleNet40) Euclidean spaces.
MNIST images are converted to 2D point clouds of digit pixel locations.
3D point clouds are sampled from mesh surfaces from ModelNet40 shapes.
In default we use 512 points for MNIST and 1024 points for ModelNet40.
In last row (ours normal) in Table 2, we use face normals as additional point features, where we also use more points (\(N = 5000\)) to further boost performance.
All point sets are normalized to be zero mean and within a unit ball.
We use a three-level hierarchical network with three fully connected layers
우리는 2D (MNIST)와 3D (ModleNet40) Euclidean spaces에서 샘플링된 point clouds를 분류하는 데 대한 네트워크를 평가한다.
MNIST images은 digit pixel locations의 2D point clouds로 변환된다.
3D point cloud는 ModelNet40 shapes의 mesh surfaces에서 샘플링됩니다.
기본적으로 MNIST의 경우 512 points를 사용하고 ModelNet40의 경우 1024 points를 사용한다.
Table 2의 last row에서는 face normals을 추가 point features으로 사용하며, 여기서 더 많은 points (\(N = 5000\))를 사용하여 성능을 더욱 향상시킨다.
모든 point sets은 0 평균이고 unit ball 내에서 정규화(normalized)된다. 우리는 three fully connected layers이 있는 three-level hierarchical network를 사용한다.
Results.
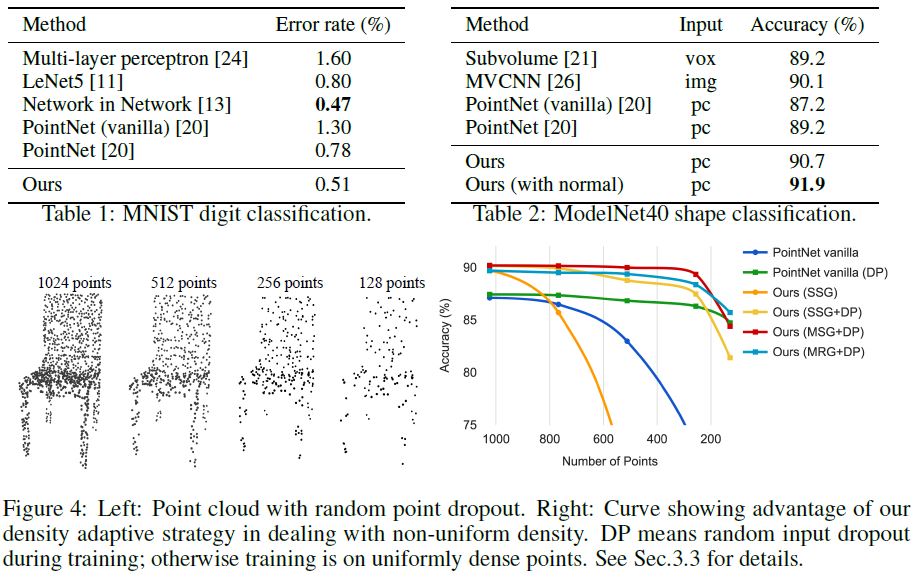
In Table 1 and Table 2, we compare our method with a representative set of previous state of the arts.
Note that PointNet (vanilla) in Table 2 is the the version in [20] that does not use transformation networks, which is equivalent to our hierarchical net with only one level.
Firstly, our hierarchical learning architecture achieves significantly better performance than the non-hierarchical PointNet [20].
In MNIST, we see a relative 60.8% and 34.6% error rate reduction from PointNet (vanilla) and PointNet to our method. In ModelNet40 classification, we also see that using same input data size (1024 points) and features (coordinates only), ours is remarkably stronger than PointNet.
Secondly, we observe that point set based method can even achieve better or similar performance as mature image CNNs.
In MNIST, our method (based on 2D point set) is achieving an accuracy close to the Network in Network CNN.
In ModelNet40, ours with normal information significantly outperforms previous state-of-the-art method MVCNN [26].
Robustness to Sampling Density Variation.
Sensor data directly captured from real world usually suffers from severe irregular sampling issues (Fig. 1).
Our approach selects point neighborhood of multiple scales and learns to balance the descriptiveness and robustness by properly weighting them.
real world에서 직접 캡처된 Sensor data는 대개 심각한 irregular sampling issues를 겪는다(Fig. 1). 우리의 접근 방식은 multiple scales의 point neighborhood을 선택하고 적절히 가중치를 부여하여 설명성과 견고성의 균형을 맞추는 방법을 배운다.
We randomly drop points (see Fig. 4 left) during test time to validate our network’s robustness to non-uniform and sparse data.
In Fig. 4 right, we see MSG+DP (multi-scale grouping with random input dropout during training) and MRG+DP (multi-resolution grouping with random input dropout during training) are very robust to sampling density variation.
MSG+DP performance drops by less than 1% from 1024 to 256 test points.
우리는 non-uniform하고 sparse이 있는 데이터에 대한 네트워크의 견고성을 검증하기 위해 테스트 시간 동안 무작위로 points를 drop한다.(see Fig. 4 left)
In Fig. 4 right에서 MSG+DP(training 중 random input dropout을 사용한 multi-scale grouping)와 MRG+DP(training 중 random input dropout을 사용한 multi-resolution grouping)가 표본 밀도 변화에 매우 강력하다는 것을 알 수 있다.
MSG+DP 성능은 1024에서 256 test points로 1% 미만으로 떨어집니다.
Moreover, it achieves the best performance on almost all sampling densities compared with alternatives.
PointNet vanilla [20] is fairly robust under density variation due to its focus on global abstraction rather than fine details.
However loss of details also makes it less powerful compared to our approach.
SSG (ablated PointNet++ with single scale grouping in each level) fails to generalize to sparse sampling density while SSG+DP amends the problem by randomly dropping out points in training time.
또한, 대안과 비교하여 거의 모든 샘플링 밀도에서 최고의 성능을 달성한다.
PointNet vanilla [20]는 정밀한 details 보다는 global abstraction에 중점을 두기 때문에 density variation 하에서 상당히 견고하다.
그러나 세부 정보가 손실되면 당사의 접근 방식에 비해 성능이 저하된다.
SSG(각 level에서 single scale grouping를 사용하는 ablated PointNet++)는 sparse sampling density로 일반화하지 못하는 반면 SSG+DP는 training 시간에 랜덤으로 points를 dropping out시켜 문제를 수정한다.
4.2 Point Set Segmentation for Semantic Scene Labeling
To validate that our approach is suitable for large scale point cloud analysis, we also evaluate on semantic scene labeling task.
The goal is to predict semantic object label for points in indoor scans.
[5] provides a baseline using fully convolutional neural network on voxelized scans.
They purely rely on scanning geometry instead of RGB information and report the accuracy on a per-voxel basis.
To make a fair comparison, we remove RGB information in all our experiments and convert point cloud label prediction into voxel labeling following [5].
We also compare with [20].
The accuracy is reported on a per-voxel basis in Fig. 5 (blue bar).
Our approach outperforms all the baseline methods by a large margin.
In comparison with [5], which learns on voxelized scans, we directly learn on point clouds to avoid additional quantization error, and conduct data dependent sampling to allow more effective learning.
Compared with [20], our approach introduces hierarchical feature learning and captures geometry features at different scales.
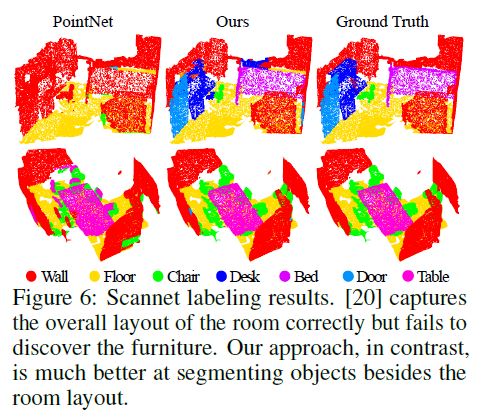
This is very important for understanding scenes at multiple levels and labeling objects with various sizes. We visualize example scene labeling results in Fig. 6.
Robustness to Sampling Density Variation
To test how our trained model performs on scans with non-uniform sampling density, we synthesize virtual scans of Scannet scenes similar to that in Fig. 1 and evaluate our network on this data.
We refer readers to supplementary material for how we generate the virtual scans.
We evaluate our framework in three settings (SSG, MSG+DP, MRG+DP) and compare with a baseline approach [20].
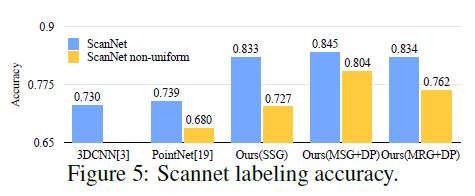
Performance comparison is shown in Fig. 5 (yellow bar).
We see that SSG performance greatly falls due to the sampling density shift from uniform point cloud to virtually scanned scenes.
MRG network, on the other hand, is more robust to the sampling density shift since it is able to automatically switch to features depicting coarser granularity when the sampling is sparse.
Even though there is a domain gap between training data (uniform points with random dropout) and scanned data with non-uniform density, our MSG network is only slightly affected and achieves the best accuracy among methods in comparison.
These prove the effectiveness of our density adaptive layer design.
4.3 Point Set Classification in Non-Euclidean Metric Space
In this section, we show generalizability of our approach to non-Euclidean space.
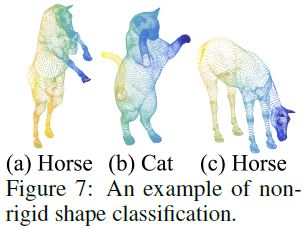
In non-rigid shape classification (Fig. 7), a good classifier should be able to classify (a) and (c) in Fig. 7 correctly as the same category even given their difference in pose, which requires knowledge of intrinsic structure.
Shapes in SHREC15 are 2D surfaces embedded in 3D space.
Geodesic distances along the surfaces naturally induce a metric space.
We show through experiments that adopting PointNet++ in this metric space is an effective way to capture intrinsic structure of the underlying point set.
For each shape in [12], we firstly construct the metric space induced by pairwise geodesic distances.
We follow [23] to obtain an embedding metric that mimics geodesic distance.
Next we extract intrinsic point features in this metric space including WKS [1], HKS [27] and multi-scale Gaussian curvature [16].
We use these features as input and then sample and group points according to the underlying metric space.
In this way, our network learns to capture multi-scale intrinsic structure that is not influenced by the specific pose of a shape.
Alternative design choices include using XY Z coordinates as points feature or use Euclidean space \(\mathbb{R}^3\) as the underlying metric space.
We show below these are not optimal choices.
Results.
We compare our methods with previous state-of-theart method [14] in Table 3. [14] extracts geodesic moments as shape features and use a stacked sparse autoencoder to digest these features to predict shape category.
Our approach using non-Euclidean metric space and intrinsic features achieves the best performance in all settings and outperforms [14] by a large margin.
Comparing the first and second setting of our approach, we see intrinsic features are very important for non-rigid shape classification.
XY Z feature fails to reveal intrinsic structures and is greatly influenced by pose variation.
Comparing the second and third setting of our approach, we see using geodesic neighborhood is beneficial compared with Euclidean neighborhood.
Euclidean neighborhood might include points far away on surfaces and this neighborhood could change dramatically when shape affords non-rigid deformation.
This introduces difficulty for effective weight sharing since the local structure could become combinatorially complicated.
Geodesic neighborhood on surfaces, on the other hand, gets rid of this issue and improves the learning effectiveness.
4.4 Feature Visualization.
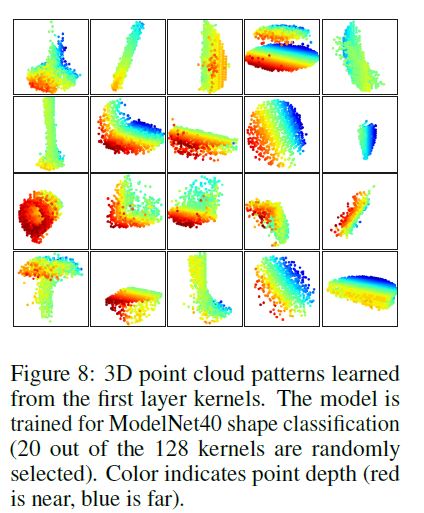
In Fig. 8 we visualize what has been learned by the first level kernels of our hierarchical network.
We created a voxel grid in space and aggregate local point sets that activate certain neurons the most in grid cells (highest 100 examples are used).
Grid cells with high votes are kept and converted back to 3D point clouds, which represents the pattern that neuron recognizes.
Since the model is trained on ModelNet40 which is mostly consisted of furniture, we see structures of planes, double planes, lines, corners etc. in the visualization.
5 Related Work
The idea of hierarchical feature learning has been very successful.
Among all the learning models, convolutional neural network [10; 25; 8] is one of the most prominent ones.
However, convolution does not apply to unordered point sets with distance metrics, which is the focus of our work.
A few very recent works [20; 28] have studied how to apply deep learning to unordered sets.
They ignore the underlying distance metric even if the point set does possess one. As a result, they are unable to capture local context of points and are sensitive to global set translation and normalization.
In this work, we target at points sampled from a metric space and tackle these issues by explicitly considering the underlying distance metric in our design.
Point sampled from a metric space are usually noisy and with non-uniform sampling density.
This affects effective point feature extraction and causes difficulty for learning.
One of the key issue is to select proper scale for point feature design.
Previously several approaches have been developed regarding this [19; 17; 2; 6; 7; 30] either in geometry processing community or photogrammetry and remote sensing community.
In contrast to all these works, our approach learns to extract point features and balance multiple feature scales in an end-to-end fashion.
In 3D metric space, other than point set, there are several popular representations for deep learning, including volumetric grids [21; 22; 29], and geometric graphs [3; 15; 33].
However, in none of these works, the problem of non-uniform sampling density has been explicitly considered.
6 Conclusion
In this work, we propose PointNet++, a powerful neural network architecture for processing point sets sampled in a metric space.
PointNet++ recursively functions on a nested partitioning of the input point set, and is effective in learning hierarchical features with respect to the distance metric.
To handle the non uniform point sampling issue, we propose two novel set abstraction layers that intelligently aggregate multi-scale information according to local point densities.
These contributions enable us to achieve state-of-the-art performance on challenging benchmarks of 3D point clouds.
In the future, it’s worthwhile thinking how to accelerate inference speed of our proposed network especially for MSG and MRG layers by sharing more computation in each local regions.
It’s also interesting to find applications in higher dimensional metric spaces where CNN based method would be computationally unfeasible while our method can scale well.
Acknowledgement.
The authors would like to acknowledge the support of a Samsung GRO grant, NSF grants IIS-1528025 and DMS-1546206, and ONR MURI grant N00014-13-1-0341.