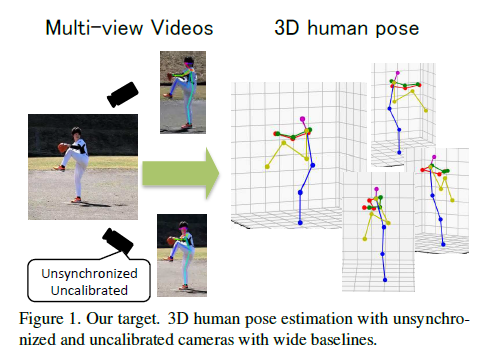
Human Pose as Calibration Pattern; 3D Human Pose Estimation with Multiple Unsynchronized and Uncalibrated Cameras
.
Takahashi, Kosuke, et al. “Human pose as calibration pattern; 3D human pose estimation with multiple unsynchronized and uncalibrated cameras.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops. 2018. paper
Abstract
This paper proposes a novel algorithm of estimating 3D human pose from multi-view videos captured by unsynchronized and uncalibrated cameras.
In a such configuration, the conventional vision-based approaches utilize detected 2D features of common 3D points for synchronization and camera pose estimation, however, they sometimes suffer from difficulties of feature correspondences in case of wide baselines.
For such cases, the proposed method focuses on that the projections of human joints can be associated each other robustly even in wide baseline videos and utilizes them as the common reference points.
To utilize the projections of joint as the corresponding points, they should be detected in the images, however, these 2D joint sometimes include detection errors which make the estimation unstable.
For dealing with such errors, the proposed method introduces two ideas.
The first idea is to relax the reprojection errors for avoiding optimizing to noised observations.
The second idea is to introduce an geometric constraint on the prior knowledge that the reference points consists of human joints.
We demonstrate the performance of the proposed algorithm of synchronization and pose estimation with qualitative and quantitative evaluations using synthesized and real data.
본 논문은 unsynchronized 및 uncalibrated cameras에 의해 캡처된 multi-view videos에서 3D human pose를 추정하는 새로운 알고리듬을 제안한다.
이러한 구성에서 기존의 vision-based approaches는 synchronization 및 camera pose estimation을 위해 common 3D points의 detected 2D features을 활용하지만, wide baselines의 경우 feature 대응의 어려움을 겪는 경우가 있다.
이러한 경우 제안된 방법은 wide baseline videos에서도 human joints의 projections을 서로 robustly하게 연관시킬 수 있다는 점에 초점을 맞추고 이를 common reference points으로 활용한다.
joint의 projections을 corresponding points로 활용하기 위해서, images에서 검출해야 하지만, 이러한 2D joint는 때떄로 estimation을 불안정하게 만드는 detection errors가 포함되는 경우도 있다.
이러한 errors를 처리하기 위해 제안된 방법은 두 가지 아이디어를 소개한다.
The first idea는 noised observations을 optimizing하는 것을 피하기 위해 reprojection errors를 완화하는 것이다.
The second idea는 human joints로 구성되는 reference points의 prior knowledge에 대한 geometric constraint를 도입하는 것이다.
우리는 synthesized 및 real data를 사용한 정성적 및 정량적 평가로 제안된 pose estimation과 synchronization 알고리듬의 성능을 입증한다.
1. Introduction
Measuring 3D human pose is important for analyzing the mechanics of the human body in various research fields, such as biomechanics, sports science and so on.
In general, some additional devices, e.g. optical markers [1] and inertial sensors [2], are introduced for measuring 3D human pose.
While these approaches have advantages in terms of high estimation quality, i.e. precision and robustness, it is sometimes difficult to utilize them in some practical scenarios, such as monitoring people in daily life or evaluating the performance of each player in a sports game, due to inconveniences of installing the devices.
To estimate 3D human pose in such cases, vision-based motion capture techniques have been studied in the field of computer vision [9].
Basically, they utilize multi-view cameras or depth sensors and assume that they are synchronized and calibrated beforehand.
Such synchronization and calibration are troublesome to establish and maintain; typically, the cameras are connected by wires and capture the same reference object.
Some 2D local features based synchronization and calibration methods have also been proposed for easy-to-use multi-view imaging systems in case for which the preparation cannot be done.
However, they sometimes suffer from difficulties of feature correspondences in case for which the multiple cameras are scattered with wide baselines, which the erroneous correspondences affect the stability and precision of estimation severely.
이러한 경우 3D human pose를 estimate하기 위해, computer vision 분야에서 vision-based motion capture techniques이 연구되었다[9].
기본적으로 multi-view cameras나 depth sensors를 활용하고 사전에 synchronized 및 calibrated된 것으로 가정한다.
이러한 synchronization 및 calibration은 설정 및 유지보수가 어렵다; 일반적으로 카메라는 와이어로 연결되어 same reference object를 캡처한다.
준비를 할 수 없는 경우에 사용하기 쉬운 multi-view imaging systems을 위해 Some 2D local features based synchronization and calibration methods도 제안되었다.
그러나, 그들은 때때로 multiple cameras가 wide baselines으로 흩어져 있는 경우 형상 대응의 어려움을 겪으며, 잘못된 대응은 추정의 안정성과 정밀도에 심각한 영향을 미친다.
This paper addresses the problem of 3D human pose estimation from multi-view videos captured by unsynchronized and uncalibrated cameras with wide baselines.
The key feature of this paper is its focus on using the projections of human joints to derive robust point associations for use as common reference points.
To detect the projections of human joints, some 2D form of pose detector is needed [7,24,25], however, 2D joint positions sometime include detection errors which make the estimation unstable.
To deal with such errors, the proposed method introduces two ideas.
The first idea is to relax the reprojection errors to avoid the optimization of noisy observations.
The second idea is to introduce a geometric constraint based on the a priori knowledge that the reference points are actually human joints.
본 논문은 wide baselines을 가진 unsynchronized 및 uncalibrated된 cameras에 의해 캡처된 multi-view videos에서 3D human pose estimation문제를 다룬다.
본 논문의 key feature은 common reference points로 사용하기 위한 robust point 연관성을 도출하기 위해 human joints의 projections을 사용하는 데 초점을 맞춘다는 것이다.
human joints의 projections을 감지하려면, pose detector의 어떤 2D form이 필요하지만 [7,24,25], 그러나 2D joint positions에는 estimation이 불안정해지는 detection errors가 포함되는 경우도 있다.
이러한 errors를 처리하기 위해, 제안된 방법은 두 가지 아이디어를 도입한다.
첫 번째 아이디어는 noisy observations의 optimization을 피하기 위해 reprojection errors를 완화하는 것이다.
두 번째 아이디어는 reference points기 실제로 human joints라는 priori knowledge에 기초한 geometric constraint을 도입하는 것이다.
The key contribution of this paper is to propose a novel algorithm for 2D human joint based multi-camera synchronization, camera pose estimation and 3D human pose estimation.
This algorithm enables us to obtain 3D human pose easily and stably even in a practical and challenging scenes, such as sports games.
본 논문의 key contribution은 2D human joint기반 multi-camera synchronization와 camera pose estimation 그리고 3D human pose estimation을 위한 새로운 algorithm을 제안하는 것이다.
이 알고리듬을 사용하면 스포츠 게임과 같은 실용적이고 도전적인 장면에서도 쉽고 안정적으로 3D 휴먼 포즈를 얻을 수 있다.
The reminder of this paper is organized as follow.
Section 2 reviews related works in terms of synchronization, extrinsic calibration and human pose estimation.
Section 3 introduces our proposed algorithm using the detected 2D joint positions as the corresponding points in multi-view images.
Section 4 reports the performance evaluations and Section 5 provides discussions on the proposed method.
Section 6 concludes this paper.
2. RelatedWorks
This section introduces the related works of our research in terms of (1) camera synchronization, (2) extrinsic camera calibration, and (3) human pose estimation.
Camera Synchronization Multiple camera synchronization significantly impacts the estimation precision of multiview applications, such as 3D reconstruction.
In general, the cameras are wired and receive a trigger signal from an external sensor telling the camera when to acquire an image.
However, these wired connections can be troublesome to establish when the cameras are widely scattered as happens when capturing a sports games.
Multiple camera synchronization은 3D reconstruction 같은 multiview applications의 estimation precision에 큰 영향을 미친다.
일반적으로 카메라는 유선 연결되고 외부 센서로부터 트리거 신호를 수신하여 이미지를 획득할 시기를 알려준다.
그러나 이러한 유선 연결은 스포츠 경기를 캡처할 때처럼 카메라가 널리 분산되어 있을 때 설정하기 어려울 수 있다.
Audio-based approaches [9,18] estimate the time shift of multi-view videos in a software post-processing step, however, the significant difference in camera position degrades the estimation precision due to the delay in sound arrival.
Audio-based approaches [9,18]은 software post-processing step에서 multi-view videos의 time shift를 estimate하지만, camera position의 상당한 차이는 음향 도착 지연으로 인해 estimation precision를 저하시킨다.
Some image-based methods [3, 22] are able to synchronize the cameras even in such cases.
Cenek et al. [3] estimates the time shift by using epipolar geometry on the corresponding points in the multi-view images.
Tamaki et al. [22] detected the same table tennis ball in sequential frames and utilized them to establish point correspondences for computing epipolar geometry.
Given the scale of the capture environment envisaged, our method is also based on epipolar geometry and so uses detected 2D joint positions as the corresponding points.
일부 image-based methods [3, 22]은 그러한 경우에도 cameras를 synchronize할 수 있다.
Cenek 외 [3]은(는) multi-view images의 해당 점에 대해 epipolar geometry를 사용하여 시간 이동을 추정한다.
Tamaki 외 [22] sequential frames에서 동일한 탁구공을 검출하여 이를 활용하여 epipolar geometry 계산을 위한 point correspondences을 설정하였다.
예상되는 캡처 환경의 척도를 고려할 때, 우리의 방법은 또한 epipolar geometry을 기반으로 하므로 detected 2D joint positions를 corresponding points으로 사용한다.
Extrinsic Camera Calibration Extrinsic camera calibration is an essential technique for 3D analysis and understanding from multi-view videos and various proposals have been made for various camera settings.
Most proposals utilize detected 2D features, such as chess board corners or local features, e.g. SIFT [13], as the corresponding points.
These approaches have difficulty in establishing reliable feature correspondence if the multiple cameras are scattered with wide baselines, as erroneous correspondences degrade the stability and precision of estimation severely.
Extrinsic camera calibration은 multi-view videos에서 3D 분석과 이해를 위한 필수적인 기술이며 다양한 camera settings에 대한 다양한 제안이 이루어졌다.
대부분의 제안은 chess board corners나 local features(예: SIFT [13])과 같은 detected 2D features을 corresponding points로 활용한다.
이러한 approaches는 erroneous correspondences가 estimation의 stability와 precision이 심각하게 저하되기 때문에, multiple cameras가 wide baselines에 산재해 있는 경우 신뢰할 수 있는 feature correspondence을 설정하는데 어려움을 겪는다.
For such cases, some studies utilize a priori knowledge of the scene.
Huang et al. [11] use the trajectories of pedestrians in calibrating multiple fixed cameras based on the assumption that the cameras can capture the same pedestrians for a long time.
Namdar et al. [10] assume that the cameras capture a sport scene in a stadium and calibrate them by introducing vanishing points computed from the lines on the sports field.
이러한 경우, 일부 연구는 장면의 priori knowledge을 활용한다.
Huang 외 [11] 카메라가 오랫동안 동일한 보행자를 포착할 수 있다는 가정에 기초하여, trajectories of pedestrians in calibrating multiple fixed cameras을 사용한다.
Namdar 외 [10] cameras가 경기장의 스포츠 장면을 캡처하고 스포츠 필드의 라인에서 계산된 vanishing points를 도입함으로써 cameras을 calibrate한다고 가정한다.
In addition, some studies [6, 16, 20] propose calibration algorithm that utilizes a priori knowledge that the scenes contain humans.
The silhouette-based approaches [5,19] establish the correspondences between special points on the silhouette boundaries, called frontier points [8], across the multiple views.
These points are the projections of 3D points tangent to the epipolar plane.
The epipolar geometry can be recovered from the correspondences of the frontier points.
또한 일부 연구[6, 16, 20]에서는 장면에 사람이 포함되어 있다는 priori knowledge을 활용하는 calibration algorithm을 제안한다.
silhouette-based approaches [5,19]은 multiple views에 걸쳐 frontier points [8]라고 불리는 silhouette boundaries에 있는 special points 사이의 대응 관계를 설정한다.
이 점들은 epipolar plane에 접하는 3D points의 projections이다.
epipolar geometry은 frontier points의 대응으로부터 복구될 수 있다.
Puwein et al. [16] proposed using detected 2D human joints in multi-view images as common reference points and using these points to compute the extrinsic parameters.
Our method is inspired by [16].
In [16], the error function consists of reprojection error, a kinematic structure term, a smooth motion term and so on, is minimized in the bundle adjustment manner.
Our work, on the other hand, introduces a relaxed reprojection error for robust estimation in the face of very noisy data; it also solves the synchronization problem.
Puwein 외 [16]는 multi-view images에서 검출된 2D human joints응 common reference points로 사용하고 이러한 points을 사용하여 extrinsic parameters를 계산할 것을 제안하였다.
우리의 방법은 [16]에서 영감을 얻었다.
[16]에서 error function는 reprojection error, kinematic structure term, smooth motion term 등으로 구성되며 bundle 조정 방식으로 최소화된다.
반면에 우리의 연구는 매우 noisy data에도 불구하고 robust한 estimation을 위해 relaxed reprojection error를 도입하고, 또한 synchronization 문제를 해결한다.
2D Human Pose Estimation Conventional studies of 2D human pose estimation problem fall into two basic groups: pictral structure approach [4, 15], in which spatial correlations between each part are expressed as a tree-structured graphical model with kinematic priors that couple connected limbs, and hierarchical model approach [21, 23], which represents the relationships between parts at different scales and sizes in a hierarchical tree structure.
2D human pose estimation 문제에 대한 기존 연구는 두 가지 기본 그룹으로 나뉜다:
- pictral structure approach [4, 15]에서 각 부분 사이의 공간적 상관 관계는 연결된 팔다리를 결합하는 kinematic priors을 가진 tree-structured graphical model로 표현된다.
- hierarchical model approach [21, 23], hierarchical tree structure에서 서로 다른 scales와 sizes의 parts 사이의 relationships을 represents한다.
Given the rapid improvement in neural network techniques, a lot of neural network based 2D pose detectors have been proposed [7,24,25].
Toshev et al. [24] solve 2D human pose as a regression problem by introducing the AlexNet architecture, which was originally used for object recognition.
Wei et al. [25] achieve high precise pose estimation by introducing CNN to the Pose Machine [17].
Caoet al. [7] consider the connectivity of each joint by introducing a part affinity field to the work of [25]; they achieve robust estimation of multi-person pose in real time.
신경망 기법의 급속한 개선을 고려할 때, 많은 신경망 기반 2D pose detectors가 제안되었다[7,24,25].
Toshev 외 [24]는 원래 object recognition에 사용되었던 AlexNet architecture를 도입하여 regression 문제로서 2D human pose를 해결한다.
Wei 외 [25]는 CNN을 Pose Machine에 도입하여 high precise pose estimation을 달성한다[17].
Caoet 외 [7]는 [25]의 작업에 part affinity field를 도입하여 각 joint의 연결성을 고려하며, 실시간으로 multi-person pose의 robust한 estimation을 달성한다.
3. Proposed Method
This section describes our proposed method for estimating 3D human pose with unsynchronized and uncalibrated multiple cameras with wide baselines.
3.1. Problem Formulation
This paper assumes that a human body is captured by multiple unsynchronized and uncalibrated cameras.
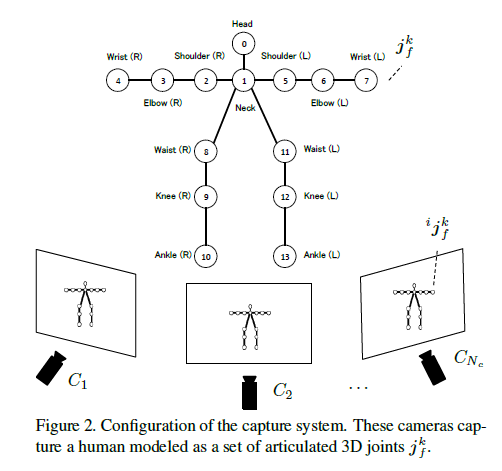
As illustrated in Figure 2, the human body is modeled as a set of articulated 3D joints.
The 3D position of the \(k\) th joint and its 2D projection onto the image plane of the \(i\)th camera, \(C_i\), in frame \(f\) are represented as \(J = {j^k_f}, k \in [1, · · · ,N_J]\) and i\(j^k_f , i \in [1, · · · ,N_c,N_c ≥ 2]\) respectively.
Let \(P = \{R_i, t_i\}\) denote the rotation matrix and translation vector, that is the extrinsic parameters of \(i\)th camera \(C_i\); they satisfy, \(p^{C_i} = R_ip^W + t_i \tag{1}\)
where \(p^{C_i}\) and \(p^W\) denote the coordinates of 3D point \(p\) in the \(C_i\) coordinate system and the world coordinate system respectively.
In this paper, \(C_1\) is the base camera and its coordinate system is used as the world coordinate system.
Let \(D = {d_i}\) denote the temporal difference in frame scale compared with the base camera \(C_1\).
This \(d_i\) satisfies the following equation, \(f^0_t = f^i_t + d_i \tag{2}\) where \(f^i_t\) denotes a \(t \in [1, · · · ,N_t]\) th frame of a video captured by \(C_i\).
Hereafter, \(f^0_t\) is written as \(f_t\) for simplicity.
The goal of this research is to estimate the 3D positions of human joint \(j^k_f\) , the extrinsic camera parameters \(R_i\) and \(t_i\), and temporal differences di. This paper assumes that a single human appears in the captured video, however, the proposed method can be extended to cover multiple people. This extension is discussed in Section 5.
For estimating these parameters, the proposed method regards as the human model as a reference object and takes a bundle adjustment approach by utilizing their projections i\(j^k_f\) as points for which correspondence is to be found.
The proposed method defines the following objective function, \(\arg\max_{P,J,L,D} E(P, J,L,D) \tag{3}\) where \(L\) denotes the separation of each joint pair, introduced in Section 3.1.2, and minimizes Eq.(3) over parameters \(P,J,L\) and \(D\).
This objective function consists of two major error terms as follows,
\(E(P, J,L,D) = E_{rep}(P, J,D) + E_{mdoel}(J,L,D)\) where \(E_{rep}(P, J,D)\) and \(E_{model}(J,L,D)\) represent the error terms of the reprojection error and the human model, respectively.
Following sections detail these error terms.
3.1.1 Relaxed Reprojection Error
The conventional 2D features for camera synchronization or calibration, such as chess corners, local features and so on, are detected with sub-pixel precision. On the other hand, the proposed method utilizes the 2D joint positions detected by a 2D pose estimation algorithms [7, 24, 25] as 2D features and most of these positions include detection errors of a few pixels. These detection errors severely impact the performance of the conventional bundle adjustment approach, which attempts to minimize the reprojection errors. Here, the proposed method avoids the problem of detection errors by relaxing the reprojection errors.
Most conventional 2D pose estimation techniques such as [7, 24, 25] estimate a confidence map for each joint and define the 2D joint position as the peak of the map as illustrated in Figure 3. Following this idea, the proposed method uses the confidence map to relax the reprojection error; that is, the influence of the reprojection error is weakened when the reprojected point is in an area of high-confidence and enhanced in when the reprojected point is in an area of lowconfidence. The proposed method assumes that the highconfidence area in the confidence map follows a normal distribution and defines the reprojection error term as follows, \[E_{rep}(P,J,D) = \frac{1}{N_rep} \sum^{N_t}_{t=0} \sum^{N_c}_{i=0} \sum^{N_j}_{k=0} g(^kj^i_{f_t},^k\hat{j}^i_{f_t}) \tag{5}\]
where \(Nrep = N_t \times N_c \times N_j\) and \(^k\hat{j}^i_{f_t}\) denote the reprojection of \(^kj^i_{f_t}\) computed from \(P, J\) and \(D,\) and \[g(x,x') = (n(0) - n(e_{rep}(x,x')))e_{rep}(x,x'), \tag{6}\] \[e_{rep}(x,x) = ||x-x'||. \tag{7}\]
\(n(x)\) denotes the probability density function of normal distribution \(N(\mu_p, \sigma^2_p)\) and \(\||x|\|\) denotes the \(L^2\)-norm of x.
3.1.2 Constraints on Human Joints
The proposed method assumes that the multi-cameras capture a human body and introduces constraints based on a priori knowledge as \(E_{model}(J,L,D)\). Error term \(E_{model}(J,L,D)\) has two terms as follows, \[E_{model}(J,L,D) = E_{length}(J,L,D) + E_{motion}(J,D). \tag{8}\]
The following sections describe these error terms in detail.
Constraint on Length of a Joint Pair The pair of the \(k\) th joint and the \(k′\) joint is denoted as \(⟨k, k′⟩\) in Figure 2.
The pairs of ⟨2, 3⟩ and ⟨8, 9⟩ can be recognized as the humerus and femur, respectively, and the length between the 3D joints on each bone are taken to be constant over time. Here, the proposed method assumes the joint pairs P = {⟨0, 1⟩, ⟨1, 2⟩, ⟨1, 5⟩, ⟨2, 3⟩, ⟨3, 4⟩, ⟨5, 6⟩, ⟨6, 7⟩, ⟨8, 9⟩, ⟨8, 11⟩, ⟨9, 10⟩, ⟨11, 12⟩, ⟨12, 13⟩} has consistent length and introduce the error term \(E_{length}(J,L,D)\) as follows, \[E_{length}(J,L,D) = \sum^{N_t}_t \sum P |||j^k_t − j^{k′}_t || − l(⟨k, k′⟩)|, \tag{9}\]
where \(l(⟨k, k′⟩)\) represents the distance between joint pair \(⟨k, k′⟩\) and \(L = {l(⟨k, k′⟩)}\).
Constraint on Smooth Motion of Each Joint The proposed method introduces a constraint on the smooth motion of a joint based on the observation that the 3D positions the joints do change drastically in sequential frames. The proposed method assumes that the local motion of each joint can be modeled as the linear motion created by uniform acceleration and introduces the following error term, \[E_{motion}(J,D) = \frac{1}{N_t \times N_j} u(j^k_t). \tag{10}\]
\(u(j^k_t)\) represents the third order differential value of \(j^k_t\).
The minimization of \(u(j^k_t)\) forces the second order differential value of \(j^k _t\) , that is the acceleration, to be consistent in sequential frames.
3.2. Algorithm
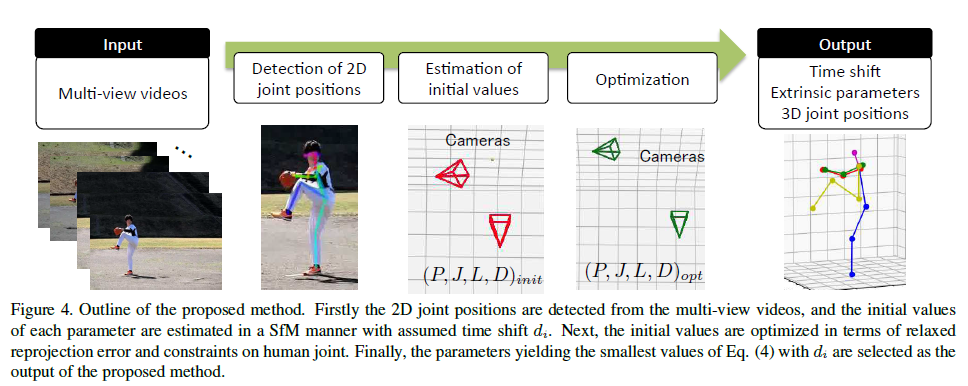
Figure 4 illustrates the processing flow of the proposed method.
First, it detects 2D joint positions from the input multi-view videos using a 2D pose detector such as [7,24,25].
Since the 2D pose detector output includes detection errors and joint detection sometimes fails due to self-occlusion, the proposed method applies a median filter after applying a cubic spline interpolation method to the output data.
Next, select two cameras and the initial values of each parameter are estimated by the standard SfM approach using assumed time shift \(d_i\); that is, it estimates the essential matrix for selected cameras, decomposes it into the extrinsic parameters, and estimates 3D joint positions through triangulation.
The extrinsic camera parameters of the other cameras are estimated by solving PnP problems [12].
Then, Eq.(4) is computed using the initial parameters and minimized by the Levenberg-Marquardt algorithm over parameters \(P\), \(J\), and \(L\).
Finally, the parameters yielding the smallest value of Eq. (4) with \(d_i\) are selected as the optimized parameters.
4. Evaluations
This section describes the performance evaluations of the proposed method with synthesized data and real data.
4.1. Evaluations with Synthesized Data
4.1.1 Experimental Environment
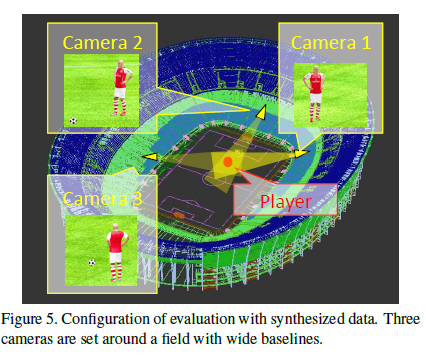
Figure 5 illustrates the evaluation setup used with synthesized data. The three unsynchronized cameras are set around a large field with baselines of about 50 ∼ 100m. These cameras capture 1920 × 1080 resolution videos with 60 frame rate. Their focal length and optical center, that is intrinsic parameters, are set to 16000 and (960, 540) respectively. The ground truth of 3D joint is synthesized from the motion capture data. The input data, the projections of the 3D joint positions, is perturbed by the addition of zero-mean Gaussian noise whose standard deviation \(\sigma(0 ≤ \sigma ≤ 8)\).
The input data also includes 10% detection failures.
4.1.2 Results
Figure 6 plots the average errors of synchronization, extrinsic parameters, and 3D joint positions for 10 trials at each noise level. From these results, we can see that all methods estimate the time shift with error of 0.006 ∼ 0.012 seconds. As to the extrinsic parameters, the proposed method offers robust estimation even if large detection error is assumed while the conventional methods suffer degraded performace. Especially, Method2 significantly degrades in $\sigma > 1$ cases. We consider that the reason is that the Method2, which minimizes the reprojection errors strictly, is significantly affected by the noise and detection failures. The proposed method estimates 3D joint positions robustly while the Method1 degrades with noisy data. Method2 also estimates 3D joint positions with comparable precisions to the proposed method in spite of its degraded extrinsic parameters. This is considered that the adjusting the scale and initial position in case of evaluating the 3D positions absorbs this degradation.
Figure 7 renders one example of the estimated camera positions and 3D joint positions in 3D space with $\sigma = 5$. This figure shows that the proposed method estimates reasonable camera positions and 3D joints.
From the above, we can conclude that the proposed method is more robust than the conventional methods even if the input data includes significant noise, especially in terms of the extrinsic parameters.
4.2. Evaluations with Real Data
This section demonstrates that the proposed method works with real data in a practical scenario.
4.2.1 Experimental Environment
Figure 8 shows the configuration of the evaluation that used real data. The two cameras (CASIO EX100) with 640 × 480 resolution and 120 fps were set with a wide baseline. Camera 0 and Camera 1 had focal lengths of 200mm and 165mm, respectively. The input video consisted of 1000 frames, that is about 8.3 seconds. These cameras captured one player throwing a ball. In the 2D pose estimation step, Cao et al. [7]’s method is utilized. This evaluation used, in addition to Method1 and Method2 introduced in Section 4.1, Zhang’s method [26] as benchmarks.
To demonstrate the performance of the proposed algorithm, the following two conventional methods are evaluated with same input data,
Method1: Initial values
As described in Section 3.2, each parameter can be linearly estimated in a conventional structure-from-motion manner. As to Method1, the evaluation function for selecting appropriate time shift is defined as the reprojection error, that is the parameters with smallest reprojection error are the output of Method1.
Method2: Bundle Adjustment
Method2 uses the bundle adjustment approach to estimate the parameters, each parameter is optimized by minimizing the reprojection errors. Here, Method2 uses the Levenberg-Marquardt algorithm for optimization. Method2 also utilizes the reprojection error as the evaluation function for selecting the appropriate time shift.
In this evaluation, each parameter is evaluated with following error functions. The error of time shift Ef is defined as the average of absolute error (millisecond time scale) as follows, \[E_f = \frac{1}{N_c} \sum^{N_c}_{i=1} |f_i - f_{ig}|, \tag{11}\]
where the parameter with subscript \(g\) represents the ground truth.
The error of rotation matrix \(E_R\) is defined as the Riemannian distance [14].
4.2.2 Results
Table 1 reports the estimation error of extrinsic parameters between each method and [26]. Figure 9 visualizes the estimated camera positions and 3D joint positions in 3D space. In Figure 9, while the camera positions estimated by Method1, Zhang’s method and the proposed method are almost same, that of Method2 diverged significantly. The reason is that the detected 2D poses include severe noise and Method2, which minimizes the reprojection errors strictly, is optimized to the noisy data same as in the evaluations with synthesized data, whereas the proposed method avoids the problem by relaxing the reprojection errors. From these results, we can see that the proposed method works robustly with severely noise-degraded data in practical situations.
5. Discussion
5.1. Precision of 2D Human Pose Detector
The 2D pose detector is utilized in the first step of the proposed method and it has significant effects on the estimation precision. Here we investigate the performance of 2D pose detector [7] utilized in this paper. Table shows the average, standard deviation, smallest value and biggest value of estimation error, that is euclidean norm of 2D human pose detected by [7] and its ground truth, in 700 frames with 1920 × 1080 resolutions. In the evaluations in Section 4, the $μ_p$ and $\sigma_p$ in the relaxed reprojection error are set based on these results.
5.2. Multiplayer Cases
As introduced in Section 3.1, our algorithm assume that there is a single player in the shared field-of-view of multiple cameras, however, it can be extend to multi-player cases. By considering the multi-players, it is considered that the estimation precision by the proposed method is improved because the number of constraints increase and the 2D joint positions, which are recognized as the corresponding points, cover more wide area in image planes of each camera. To deal with multi-player cases, the person identification problem and occlusion handling are to be solved in addition. This extension is included in our future works.
6. Conclusion
This paper proposed a novel 3D human joint position estimation algorithm for unsynchronized and uncalibrated cameras with wide baselines. The method focuses on the major skeleton joints and the constancy of joint separation. The 2D human pose is detected from the multi-view images and joint position estimates are used in the structure-frommotion manner. The proposed method provides an objective function consisting of a relaxed reprojection error term and human joint error term in order to achieve robust estimation even if the input data is noisy; the objective term is optimized. Evaluations using synthesized data and real data showed that the proposed method works robustly with noise-corrupted data. Future works include evaluations that use marker-based motion capture techniques and extension to the multi-player cases.