Self-Supervised Learning of 3D Human Pose using Multi-view Geometry
.
Kocabas, Muhammed, Salih Karagoz, and Emre Akbas. “Self-supervised learning of 3d human pose using multi-view geometry.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2019. paper
Abstract
Training accurate 3D human pose estimators requires large amount of 3D ground-truth data which is costly to collect.
Various weakly or self supervised pose estimation methods have been proposed due to lack of 3D data.
Nevertheless, these methods, in addition to 2D ground-truth poses, require either additional supervision in various forms (e.g. unpaired 3D ground truth data, a small subset of labels) or the camera parameters in multiview settings.
To address these problems, we present EpipolarPose, a self-supervised learning method for 3D human pose estimation, which does not need any 3D ground-truth data or camera extrinsics.
정확한 3D human pose estimators를 훈련하려면 수집 비용이 많이 드는 large amount of 3D ground-truth data가 필요하다. 다양한 weakly or self supervised pose estimation methods가 제안되어왔다. 그럼에도 불구하고 이러한 방법은 2D ground-truth poses 외에도 다양한 형태(예: unpaired 3D ground truth data, a small subset of labels)의 additional supervision이나 multiview settings의 camera parameters를 필요로 한다. 이러한 문제를 해결하기 위해, 우리는 3D ground-truth data나 camera extrinsics이 전혀 필요하지 않은 3D human pose estimation을 위한 self-supervised learning method인 EpipolarPose를 제시한다.
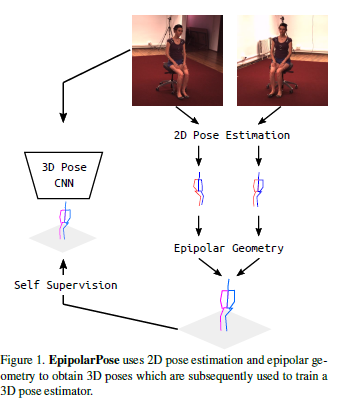
During training, EpipolarPose estimates 2D poses from multi-view images, and then, utilizes epipolar geometry to obtain a 3D pose and camera geometry which are subsequently used to train a 3D pose estimator.
We demonstrate the effectiveness of our approach on standard benchmark datasets (i.e. Human3.6M and MPI-INF-3DHP) where we set the new state-of-the-art among weakly/self-supervised methods.
Furthermore, we propose a new performance measure Pose Structure Score (PSS) which is a scale invariant, structure aware measure to evaluate the structural plausibility of a pose with respect to its ground truth.
Code and pretrained models are available at https://github.com/mkocabas/EpipolarPose
training 중에 EpipolarPose는 multi-view images에서 2D poses를 추정한 다음 epipolar geometry를 사용하여 3D pose와 카camera geometry를 얻고 이후 3D pose estimator를 훈련하는 데 사용된다.
우리는 weakly/self-supervised methods중 새로운 state-of-the-art임을 보여주기위해 standard benchmark datasets(즉, Human3.6M과 MPI-INF-3DHP)에 대한 우리의 approach 효과를 보여준다.
또한, 우리는 그것의 ground truth에 대한 pose의 구조적 신뢰성을 평가하기 위한 ‘스케일 불변’, ‘‘구조 인식 측정’인 새로운 성능 측정 포즈 구조 점수(PSS)를 제안한다.
1. Introduction
Human pose estimation in the wild is a challenging problem in computer vision.
Although there are large-scale datasets [2, 20] for two-dimensional (2D) pose estimation, 3D datasets [15, 23] are either limited to laboratory settings or limited in size and diversity.
Since collecting 3D human pose annotations in the wild is costly and 3D datasets are limited, researchers have resorted to weakly or self supervised approaches with the goal of obtaining an accurate 3D pose estimator by using minimal amount of additional supervision on top of the existing 2D pose datasets.
Various methods have been developed to this end.
These methods, in addition to ground-truth 2D poses, require either additional supervision in various forms (such as unpaired 3D ground truth data[41], a small subset of labels [31]) or (extrinsic) camera parameters in multiview settings [30].
To the best of our knowledge, there is only one method [9] which can produce a 3D pose estimator by using only 2D ground-truth.
In this paper, we propose another such method.
in the wild의 Human pose estimation은 computer vision에서 challenging problem이다.
two-dimensional (2D) pose estimation을 위한 large-scale datasets [2, 20]가 있지만, 3D datasets [15, 23]는 실험실 설정으로 제한되거나 크기와 다양성이 제한된다.
in the wild에서 3D human pose annotations을 수집하는 것은 비용이 많이 들고3D datasets가 제한적이기 때문에, 연구원들은 기존의 2D pose datasets 위에 최소한의 additional supervision을 사용하여 정확한 3D pose estimator를 얻는 것을 목표로 weakly or self supervised approaches에 의존했다.
이를 위해 다양한 방법이 개발되었다.
이러한 방법은 ground-truth 2D poses 외에도 다양한 형태(unpaired 3D ground truth data[41], a small subset of labels [31]) 또는 multiview settings [30]의 (extrinsic) camera parameters의 additional supervision을 필요로 한다.
우리가 아는 한,2D ground-truth만 사용하여 3D pose estimator를 생성할 수 있는 방법은 단 하나 [9]이다.
본 논문에서, 우리는 또 다른 그러한 방법을 제안한다.
Our method, “EpiloparPose,” uses 2D pose estimation and epipolar geometry to obtain 3D poses, which are subsequently used to train a 3D pose estimator.
EpipolarPose works with an arbitrary number of cameras (must be at least 2) and it does not need any 3D supervision or the extrinsic camera parameters, however, it can utilize them if provided.
On the Human3.6M [15] and MPI-INF-3DHP [23] datasets, we set the new state-of-the-art in 3D pose estimation for weakly/self-supervised methods.
우리의 방법인 “EpiloparPose”는 2D pose estimation과 epipolar geometry을 사용하여 3D poses를 얻으며, 이후 3D pose estimator를 훈련시키는 데 사용된다.
EpipolarPose는 임의의 카메라 개수(최소 2개여야 함)로 작동하며 3D supervision이나 extrinsic camera parameters가 전혀 필요하지 않지만 제공된 경우 이를 활용할 수 있다.
uman3.6M [15] 및 MPI-INF-3DHP [23] datasets에서, 우리는 weakly/self-supervised methods에 대한new state-of-the-art in 3D pose estimation을 설정한다.
Human pose estimation allows for subsequent higher level reasoning, e.g. in autonomous systems (cars, industrial robots) and activity recognition.
In such tasks, structural errors in pose might be more important than the localization error measured by the traditional evaluation metrics such as MPJPE (mean per joint position error) and PCK (percentage of correct keypoints).
These metrics treat each joint independently, hence, fail to asses the whole pose as a structure.
Human pose estimation은 자율 시스템(자동차, 산업용 로봇) 및 활동 인식과 같은 후속적으로 더 높은 수준의 추론을 가능하게 한다.
이러한 작업에서, pose에서 structural errors는 MPJPE(mean per joint position error) 및 PCK(percentage of correct keypoints)와 같은 전통적인 평가 지표에 의해 측정된 localization error보다 더 중요할 수 있다.
이러한 metrics는 각 joint를 독립적으로 처리하므로 전체 자세를 하나의 구조로 평가하지 못한다.
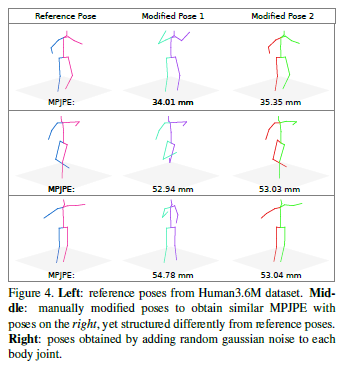
Figure 4 shows that structurally very different poses yield the same MPJPE with respect to a reference pose.
To address this issue, we propose a new performance measure, called the Pose Structure Score (PSS), which is sensitive to structural errors in pose.
PSS computes a scale invariant performance score with the capability to score the structural plausibility of a pose with respect to its ground truth.
Note that PSS is not a loss function, it is a performance measure that can be used along with MPJPE and PCK to account for structural errors made by a pose estimator.
그림 4는 구조적으로 매우 다른 포즈가 기준 포즈와 관련하여 동일한 MPJPE를 산출한다는 것을 보여준다.
이 문제를 해결하기 위해, 우리는 pose의 구조적 오류에 민감한 Pose Structure Score (PSS)라는 new performance measure을 제안한다. PSS는 그것의 ground truth에 관한 pose의 structural plausibility을 점수화하는 능력으로 scale invariant performance score를 계산한다.
PSS는 loss function이 아니라 pose estimator에 의해 이루어진 structural errors를 설명하기 위해 MPJPE 및 PCK와 함께 사용할 수 있는 performance measure이라는 점에 유의한다.
To compute PSS, we first need to model the natural distribution of ground-truth poses.
To this end, we use an unsupervised clustering method.
Let \(\textbf{p}\) be the predicted pose for an image whose ground-truth is \(\textbf{q}\).
First, we find which cluster centers are closest to \(\textbf{p}\) and \(\textbf{q}\).
If both of them are closest to (i.e. assigned to) the same cluster center, then the pose structure score (PSS) of \(\textbf{p}\) is said to be 1, otherwise 0.
Contributions Our contributions are as follows:
We present EpipolarPose, a method that can predict 3D human pose from a single-image. For training, EpipolarPose does not require any 3D supervision nor camera extrinsics. It creates its own 3D supervision by utilizing epipolar geometry and 2D ground-truth poses.
We set the new state-of-the-art among weakly/selfsupervised methods for 3D human pose estimation.
We present Pose Structure Score (PSS), a new performance measure for 3D human pose estimation to better capture structural errors.
2. Related Work
Our method, EpipolarPose, is a single-view method during inference; and a multi-view, self-supervised method during training.
Before discussing such methods in the literature, we first briefly review entirely single-view (during both training and inference) and entirely multi-view methods for completeness.
우리의 방법인 EpipolarPose는 inference에서 single-view method, training에서는 multi-view, self-supervised method이다.
literature에서 이러한 방법을 논의하기 전에 먼저 completeness을 위해 entirely single-view (during both training and inference)와 entirely multi-view methods을 간략하게 review한다.
Single-view methods In many recent works, convolutional neural networks (CNN) are used to estimate the coordinates of the 3D joints directly from images [38, 39, 40, 35, 23].
Li and Chan [19] were the first to show that deep neural networks can achieve a reasonable accuracy in 3D human pose estimation from a single image.
They used two deep regression networks and body part detection.
Tekin et al. [38] show that combining traditional CNNs for supervised learning with auto-encoders for structure learning can yield good results.
Contrary to common regression practice, Pavlakos et al. [29] were the first to consider 3D human pose estimation as a 3D keypoint localization problem in a voxel space.
Recently, “integral pose regression” proposed by Sun et al. [36] combined volumetric heat maps with a soft-argmax activation and obtained state-of-the-art results.
최근의 많은 연구에서, convolutional neural networks (CNN)은 images에서 직접 3D joints의 좌표를 추정하는 데 사용된다[38, 39, 40, 35, 23].
Li와 Chan[19]은 deep neural networks이 단일 이미지에서 3D human pose estimation을 합리적인 정확도를 달성할 수 있다는 것을 처음으로 보여주었다.
two deep regression networks와 body part detection를 사용했다.
Tekin 등[38]은 supervised learning을 위한 traditional CNNs과 structure learning을 위한 auto-encoders를 결합하면 좋은 결과를 얻을 수 있음을 보여준다.
일반적인 regression practice과는 반대로 Pavlakos 등[29]은 voxel space에서 3D human pose estimation을 3D keypoint localization problem으로 가장 먼저 고려했다.
최근 Sun 등이 제안한 “integral pose regression”[36]는 olumetric heat maps와 soft-argmax activation을 결합하고 state-of-the-art results를 얻었다.
Additionally, there are two-stage approaches which decompose the 3D pose inference task into two independent stages: estimating 2D poses, and lifting them into 3D space [8, 24, 22, 11, 46, 8, 40, 23].
Most recent methods in this category use state-of-the-art 2D pose estimators [7, 43, 25, 17] to obtain joint locations in the image plane.
Martinez et al. [22] use a simple deep neural network that can estimate 3D pose given the estimated 2D pose computed by a state-of-the-art 2D pose estimator.
Pavlakos et al. [28] proposed the idea of using ordinal depth relations among joints to bypass the need for full 3D supervision.
또한, 3D pose inference task을 두 개의 독립된 단계로 분해하는 two-stage approaches가 있다: estimating 2D poses과 lifting them into 3D space[8, 24, 22, 11, 46, 8, 40, 23].
이 category의 최신 방법은 state-of-the-art 2D pose estimators[7, 43, 25, 17]를 사용하여 이미지 plane에서 joint locations를 얻는다.
Martinez 등[22]은 state-of-the-art 2D pose estimator에 의해 계산된 estimated 2D pose가 주어진 3D pose를 추정할 수 있는 simple deep neural network을 사용한다.
Pavlakos 등 [28]은 full 3D supervision의 필요성을 bypass하기 위해 joints 사이의 ordinal depth relations를 사용하는 아이디어를 제안했다.
Methods in this category require either full 3D supervision or extra supervision (e.g. ordinal depth) in addition to full 3D supervision.
이 category의 Methods은 full 3D supervision 또는 full 3D supervision 외에 extra supervision(예: ordinal depth)을 필요로 한다.
Multi-view methods
Methods in this category require multi-view input both during testing and training.
Early work [1, 5, 6, 3, 4] used 2D pose estimations obtained from calibrated cameras to produce 3D pose by triangulation or pictorial structures model.
More recently, many researchers [10] used deep neural networks to model multi-view input with full 3D supervision.
이 category의 Methods은 testing과 training 모두 multi-view input을 필요로 한다.
초기 작업[1, 5, 6, 3, 4]은 calibrated cameras에서 얻은 2D pose estimations을 사용하여 triangulation 또는 pictorial structures model에 의한 3D pose를 생성했다.
보다 최근에는 [10] 많은 연구자가 deep neural networks를 사용하여 full 3D supervision으로 multi-view input을 모델링했다.
Weakly/self-supervised methods
Weak and self supervision based methods for human pose estimation have been explored by many [9, 31, 41, 30] due to lack of 3D annotations.
Pavlakos et al. [30] use a pictorial structures model to obtain a global pose configuration from the keypoint heatmaps of multi-view images.
Nevertheless, their method needs full camera calibration and a keypoint detector producing 2D heatmaps.
human pose estimation을 위한 Weak and self supervision based methods은 3D annotations의 부족으로 인해 [9, 31, 41, 30]에 의해 탐구되었다.
Pavlakos 등 [30]은 pictorial structures model을 사용하여 multi-view images의 keypoint heatmaps에서 global pose configuration을 얻는다.
그럼에도 불구하고, 이들의 방법은 full camera calibration과 2D heatmaps을 생성하는 keypoint detector가 필요하다.
Rhodin et al. [31] utilize multi-view consistency constraints to supervise a network.
They need a small amount of 3D ground-truth data to avoid degenerate solutions where poses collapse to a single location.
Thus, lack of in-the-wild 3D ground-truth data is a limiting factor for this method [31].
Rhodin 등 [31]은 multi-view 일관성 제약 조건을 활용하여 network를 supervise한다.
poses가 single location으로 collapse되는 degenerate solutions을 방지하기 위해 소량의 3D ground-truth data가 필요합니다.
따라서, in-the-wild 3D ground-truth data의 부족은 이 method의 limiting factor이다 [31].
Recently introduced deep inverse graphics networks [18, 44] have been applied to the human pose estimation problem [41, 9].
Tung et al. [41] train a generative adversarial network which has a 3D pose generator trained with a reconstruction loss between projections of predicted 3D poses and input 2D joints and a discriminator trained to distinguish predicted 3D pose from a set of ground truth 3D poses.
Following this work, Drover et al. [9] eliminated the need for 3D ground-truth by modifying the discriminator to recognize plausible 2D projections.
최근 도입된 deep inverse graphics networks [18, 44]가 human pose estimation problem에 적용되었다[41, 9].
Tung 등 [41]은 projections of predicted 3D poses와 input 2D joints간의 reconstruction loss로 train된 3D pose generator와 a set of ground truth 3D poses로부터 predicted 3D pose를 구별하기위해 train된 discriminator를 가지는 generative adversarial network를 train하였다. 그 다음으로, Driver 등[9]은 discriminator를 수정하여 타당한 2D projections을 인식함으로써 3D ground-truth의 필요성을 없앴다.
To the best of our knowledge, EpipolarPose and Drover et al.’s method are the only ones that do not require any 3D supervision or camera extrinsics.
While their method does not utilize image features, EpipolarPose makes use of both image features and epipolar geometry and produces much more accurate results (4.3 mm less error than Drover et al.’s method).
우리가 아는 한, EpipolarPose와 ‘Drover 등’의 방법은 3D supervision이나 camera extrinsics이 필요하지 않은 유일한 방법이다.
그들의 방법은 image features을 활용하지 않지만, EpipolarPose는 image features와 epipolar geometry을 모두 사용하며 훨씬 더 정확한 결과(‘Drover등’의 방법보다 4.3mm 더 적은 error)를 산출한다.
3. Models and Methods
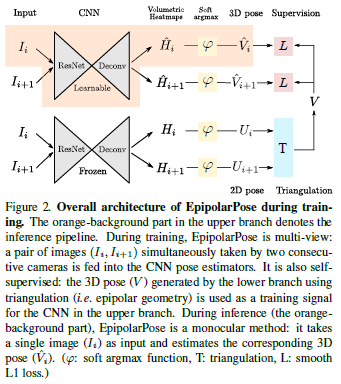
The overall training pipeline of our proposed method, EpipolarPose, is given in Figure 2. The orange-background part shows the inference pipeline. For training of EpipolarPose, the setup is assumed to be as follows. There are n cameras (\(n ≥ 2\) must hold) which simultaneously take the picture of the person in the scene. The cameras are given id numbers from 1 to \(n\) where consecutive cameras are close to each other (i.e. they have small baseline).
The cameras produce images \(I_1, I_2, . . . I_n\). Then, the set of consecutive image pairs, \(\{(I_i, I_{i+1})|i = 1, 2, . . . , n−1\}\), form the training examples.
3.1. Training
In the training pipeline of EpipolarPose (Figure 2), there are two branches each starting with the same pose estimation network (a ResNet followed by a deconvolution network [36]).
These networks were pre-trained on the MPII Human Pose dataset (MPII) [2].
During training, only the pose estimation network in the upper branch is trained; the other one is kept frozen.
EpipolarPose can be trained using more than 2 cameras but for the sake of simplicity, here we will describe the training pipeline for \(n = 2\).
For \(n = 2\), each training example contains only one image pair.
Images \(I_i\) and \(I_{i+1}\) are fed into both the 3D (upper) branch and 2D (lower) branch pose estimation networks to obtain volumetric heatmaps \(\hat{H} ,H \in mathcal{R}^{w \times h \times d}\) respectively, where \(w, h\) are the spatial size after deconvolution, \(d\) is the depth resolution defined as a hyperparameter.
After applying soft argmax activation function \(\varphi(·)\) we get 3D pose \(\hat{V} \in \mathcal{R}^{J \times 3} and 2D pose\)U \in R^{J \times 2} outputs where \(J\) is the number of body joints.
From a given volumetric heatmap, one can obtain both a 3D pose (by applying softargmax to all 3 dimensions) and a 2D pose (by applying softargmax to only \(x, y\)).
As an output of 2D pose branch, we want to obtain the 3D human pose \(V\) in the global coordinate frame.
Let the 2D coordinate of the \(j^{th}\) joint in the \(i^{th}\) image be \(U_{i,j} = [x_{i,j} , y_{i,j}]\) and its 3D coordinate be \([X_j , Y_j ,Z_j]\), we can describe the relation between them assuming a pinhole image projection model \[\begin{bmatrix} x_{i,j} \\ y_{i,j} \\ w_{i,j} \end{bmatrix} = K[R|RT] \begin{bmatrix} X_j \\ Y_j \\ Z_j \\ 1 \end{bmatrix} , K = \begin{bmatrix} f_{x} & 0 & c_x \\ 0 & f_{y} & c_y \\ 0 & 0 & 1 \end{bmatrix}, T = \begin{bmatrix} T_{x} \\ T_{y} \\ T_{z} \end{bmatrix} \tag{1}\]
where \(w_{i,j}\) is the depth of the \(j^{th}\) joint in the \(i^{th}\) camera’s image with respect to the camera reference frame, \(K\) encodes the camera intrinsic parameters (e.g., focal length \(f_x\) and \(f_y\), principal point \(c_x\) and \(x_y\)), \(R\) and \(T\) are camera extrinsic parameters of rotation and translation, respectively.
We omit camera distortion for simplicity.
When camera extrinsic parameters are not available, which is usually the case in dynamic capture environments, we can use body joints as calibration targets.
We assume the first camera as the center of the coordinate system, which means \(R\) of the first camera is identity.
For corresponding joints in \(U_i\) and \(U{i+1}\), in the image plane, we find the fundamental matrix \(F\) satisfying \(U_{i,j}FU_{i+1,j} = 0\) for \(\forall j\) using the RANSAC algorithm. From \(F\), we calculate the essential matrix \(E\) by \(E = K^TFK\).
By decomposing \(E\) with \(SVD\), we obtain 4 possible solutions to \(R\).
We decide on the correct one by verifying possible pose hypotheses by doing cheirality check.
The cheirality check basically means that the triangulated 3D points should have positive depth [26].
We omit the scale during training, since our model uses normalized poses as ground truth.
Finally, to obtain a 3D pose \(V\) for corresponding synchronized 2D images, we utilize triangulation (i.e. epipolar geometry) as follows.
For all joints in (\(I_i, I_{i+1}\)) that are not occluded in either image, triangulate a 3D point \([X_j , Y_j ,Z_j ]\) using polynomial triangulation [12].
For settings including more than 2 cameras, we calculate the vector-median to find the median 3D position.
To calculate the loss between 3D pose in camera frame \(\hat{V}\) predicted by the upper (3D) branch, we project \(V\) onto corresponding camera space, then minimize \(smooth_{L1} (V − \hat{V} )\) to train the 3D branch where \[smooth_{L1}(x)= \begin{cases} 0.5x^2 & {if |x| < 1}\\ |x| - 0.5, & {otherwise} \end{cases} \tag{2}\]
Why do we need a frozen 2D pose estimator?
In the training pipeline of EpipolarPose, there are two branches each of which is starting with a pose estimator.
While the estimator in the upper branch is trainable, the other one in the lower branch is frozen.
The job of the lower branch estimator is to produce 2D poses.
One might question the necessity of the frozen estimator since we could obtain 2D poses from the trainable upper branch as well.
When we tried to do so, our method produced degenerate solutions where all keypoints collapse to a single location.
In fact, other multi-view methods faced the same problem [31, 37].
Rhodin et al. [31] solved this problem by using a small set of ground-truth examples, however, obtaining such groundtruth may not be feasible in most of the in the wild settings.
Another solution proposed recently [37] is to minimize angular distance between estimated relative rotation \(\hat{R}\) (computed via Procrustes alignment of the two sets of keypoints) and the ground truth \(R\).
Nevertheless, it is hard to obtain ground truth \(R\) in dynamic capture setups.
To overcome these shortcomings, we utilize a frozen 2D pose detector during training time only.
3.2. Inference
Inference involves the orange-background part in Figure 2.
The input is just a single image and the output is the estimated 3D pose \(\hat{V}\) obtained by a soft-argmax activation, \(\varphi(·)\), on 3D volumetric heatmap \(\hat{H}_i\).
3.3. Refinement, an optional posttraining
In the literature there are several techniques [22, 11, 39] to lift detected 2D keypoints into 3D joints.
These methods are capable of learning generalized \(2D \rightarrow 3D\) mapping which can be obtained from motion capture (MoCap) data by simulating random camera projections.
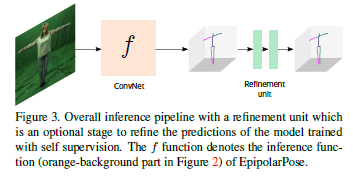
Integrating a refinement unit (RU) to our self supervised model can further improve the pose estimation accuracy.
In this way, one can train EpipolarPose on his/her own data which consists of multiple view footages without any labels and integrate it with RU to further improve the results.
To make this possible, we modify the input layer of RU to accept noisy 3D detections from EpipolarPose and make it learn a refinement strategy. (See Figure 3)
The overall RU architecture is inspired by [22, 11].
It has 2 computation blocks which have certain linear layers followed by Batch Normalization [14], Leaky ReLU [21] activation and Dropout layers to map 3D noisy inputs to more reliable 3D pose predictions.
To facilitate information flow between layers, we add residual connections [13] and apply intermediate loss to expedite the intermediate layers’ access to supervision.
3.4. Pose Structure Score
As we discussed in Section 1, traditional distance-based evaluation metrics (such as MPJPE, PCK) treat each joint independently, hence, fail to asses the whole pose as a structure.
In Figure 4, we present example poses that have the same MPJPE but are structurally very different, with respect to a reference pose.
We propose a new performance measure, called the Pose Structure Score (PSS), which is sensitive to structural errors in pose.
PSS computes a scale invariant performance score with the capability to assess the structural plausibility of a pose with respect to its ground truth.
Note that PSS is not a loss function, it is a performance score that can be used along with MPJPE and PCK to account for structural errors made by the pose estimator.
PSS is an indicator about the deviation from the ground truth pose that has the potential to cause a wrong inference in a subsequent task requiring semantically meaningful poses, e.g. action recognition, human-robot interaction.
How to compute PSS?
Implementation details
4. Experiments
Datasets. We first conduct experiments on the Human3.6M (H36M) large scale 3D human pose estimation benchmark [15]. It is one of the largest datasets for 3D human pose estimation with 3.6 million images featuring 11 actors performing 15 daily activities, such as eating, sitting, walking and taking a photo, from 4 camera views. We mainly use this dataset for both quantitative and qualitative evaluation.
We follow the standard protocol on H36M and use the subjects 1, 5, 6, 7, 8 for training and the subjects 9, 11 for evaluation.
Evaluation is performed on every \(64^{th}\) frame of the test set.
We include average errors for each method.
To demonstrate further applicability of our method, we use MPI-INF-3DHP (3DHP) [23] which is a recent dataset that includes both indoor and outdoor scenes. We follow the standard protocol: The five chest-height cameras and the provided 17 joints (compatible with H36M) are used for training. For evaluation, we use the official test set which includes challenging outdoor scenes. We report the results in terms of PCK and NPCK to be consistent with [31]. Note that we do not utilize any kind of background augmentation to boost the performance for outdoor test scenes.
Metrics. We evaluate pose accuracy in terms of MPJPE (mean per joint position error), PMPJPE (procrustes aligned mean per joint position error), PCK (percentage of correct keypoints), and PSS at scales @50 and @100.
To compare our model with [31], we measured the normalized metrics NMPJPE and NPCK, please refer to [31] for further details.
Note that PSS, by default, uses normalized poses during evaluation.
In the presented results “n/a” means “not applicable” where it’s not possible to measure respective metric with provided information, “-” means “not available”.
For instance, it’s not possible to measure MPJPE or PCK when \(R\), the camera rotation matrix, is not available.
For some of the previous methods with open source code, we indicate their respective PSS scores.
We hope, in the future, PSS will be adapted as an additional performance measure, thus more results will become available for complete comparisons.
4.1. Results
Can we rely on the labels from multi view images?
Comparison to Stateoftheart
Weakly/Self Supervised Methods
5. Conclusion
In this work, we have shown that even without any 3D ground truth data and the knowledge of camera extrinsics, multi view images can be leveraged to obtain self supervision. At the core of our approach, there is EpipolarPose which can utilize 2D poses from multi-view images using epipolar geometry to self-supervise a 3D pose estimator. EpipolarPose achieved state-of-the-art results in Human3.6M and MPI-INF-3D-HP benchmarks among weakly/self-supervised methods. In addition, we discussed the weaknesses of localization based metrics i.e. MPJPE and PCK for human pose estimation task and therefore proposed a new performance measure Pose Structure Score (PSS) to score the structural plausibility of a pose with respect to its ground truth.