2021 CVPR paper

• CanonPose: Self-Supervised Monocular 3D Human Pose Estimation in the Wild
  • Abstract
  • 1. Introduction
  • Method
    • 3.1. Reprojection
    • 3.2. View-consistency
    • 3.3. Confidence
    • 3.4 Camera-consistency
    • 3.5 Network Architecture
  • 4. Experiments
    • 4.1 Metrics
    • 4.2 Skeleton Morphing
    • 4.3 Quantitative Evaluation on Human3.6M and 3DHP
    • 4.4 Moving cameras
    • 4.5. Ablation Studies
    • 4.6. Are We Learning a Canonical Pose Basis?
  • 5. Conclusion

CanonPose: Self-Supervised Monocular 3D Human Pose Estimation in the Wild

Abstract

Single images에서 Human pose estimation은 computer vision분야에서 challenging problem으로 정확하게 해결되기위해서 많은 양의 라벨된 training data를 요구한다.
불행하게도, 여러 인간활동(예를들면 outdoor sport)와 같은 training data는 존재하지 않고 학습가능한 motion capture systems를 요구하기 어렵고 심지어 불가능하다.
우리는 unlabeled multi-view data에서 single image 3D pose estimator를 학습하는 self-supervised approach를 제안한다.
결국에, 우리는 multi-view consistency constraints를 이용해서 관찰된 2D pose를 underlying 3D pose와 camera rotation으로 disentangle(풀다)한다. To this end, we exploit multi-view consistency constraints to disentangle the observed 2D pose into the underlying 3D pose and camera rotation.

기존에 있는 methods와 대조적으로, 우리는 calibrated cameras가 필요없고 그러므로 움직이는 cameras에서 학습이 가능하다.
그럼에도 불구하고 static camera setup인 경우에, 우리는 우리의 framework안에서 multiple views에 걸쳐 constant relative camera rotations를 포함하기 위해 optional extension을 제시한다.
성공의 Key는 새롭고 unbiased reconstruction objective이다.
이것은 across views 정보와 training samples를 mix한다. Key to the success are new, unbiased reconstruction objectives that mix information across views and training samples.

1. Introduction

Human pose estimation from single images는 컴퓨터비전분야에서 진행중인 research topic이다.
이미 supervised deep learning 해결법이 많이 있는데 이것은 supervised setting에서 두드러진 결과를 성취한다. 즉, 2D와 3D annotations을 가지고 있다. 하지만 사용가능한 방대한 양의 training data에 크게 의존한다.
우리는 multi-view training dataset에서 어떠한 2D나 3D annotations을 요구하지 않고 uncalibrated cameras에 작동하는 novel self-supervised training procedure을 제안한다.
images에서 2D joint predictions을 요구하기 위해 우리는 2D annotations가 있는 서로 다른 datasets에 pre-trained된 2D human joint estimator를 사용한다.

우리의 method가 요구하는 것은 오로지 서로 다른 각도에서 중심이 되는 한 사람을 관찰하는 적어도 two temporally synchronized cameras이다.
The only requirements for our method are at least two temporally synchronised cameras that observe the person of interest from different angles.

Scene에 대한 사전지식없이, camera calibration과 intrinsics(내부파라메타)는 필요하다.

관련 연구 3D annotation이 부족한 경우 [36,34,29] 36 : Learning monocular 3d human pose estimation from multi-view images. 34 : Neural scene decomposition for multi-person motion capture. 29 : Unsupervised 3d human pose representation with viewpoint and pose disentanglement.

Unpaired 3D data인 경우[47,48,16] 47 : Repnet: Weakly supervised training of an adversarial reprojection network for 3d human pose estimation. 48 : Distill knowledge from nrsfm for weakly supervised 3d pose learning. 16 : Self-supervised 3d human pose estimation via part guided novel image synthesis.

known camera positions인 경우 [36,34] 36 : Learning monocular 3d human pose estimation from multi-view images. 34 : Neural scene decomposition for multi-person motion capture.

하지만 outdoor setting과 moving cameras애 대한 것은 없다. 오로지 3개 methods가 우리 세팅에 적용된다. [2, 14, 11] 2 : Unsupervised 3d pose estimation with geometric self-supervision. 14 : Selfsupervised learning of 3d human pose using multi-view geometry. 11 : Weaklysupervised 3d human pose learning via multi-view images in the wild. 우리는 multiple weight-sharing neural networks의 output을 섞은 self-supervised training을 제안한다. We propose a self-supervised training method which mixes outputs of multiple weight-sharing neural networks.

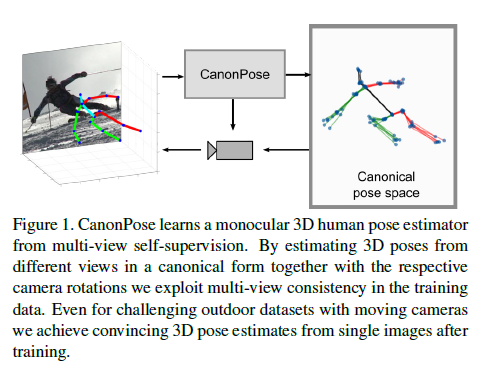
각 개별 네트워크는 single image를 input으로 하고 canonical rotation을 통해 3D pose를 output 한다. 우리는 이것을 CanonPose라고 이름지었다.

이 representation은 어떤 카메라 setup에 estimated된 모든 3D poses의 projection을 허락한다?
우리의 approach는 2개의 stages로 나눈다.

첫 stage는 MPII에 pretrained된 neural network, 우리의 경우 AlphaPose를 사용하여 image에서부터 2D human pose를 예측한다.

두번째 stage는 이 2D detections를 학습된 canonical coordinate system으로 represented된 3D pose로 lifting한다.

이것은 3D pose를 camera coordinate system으로 되돌리는 rotate를 하기위해 camera orientation을 예측한다.

first view의 3D pose와 second view에서 예측한 rotation과의 결과는 second camera coordinate system에서 rotated된 pose이다.

In other words, both 3D poses in the pose coordinate system should be equal and the predicted rotations project it back into the respective camera coordinate systems.

This enables the definition of a reprojection loss for each original and newly combined reprojection.

For static camera setups we propose an optional reprojection loss that is computed by mixing relative camera rotations between samples in a training batch.

추가적으로 기존 self-supervised approaches과 대조적으로, we make use of the confidences that are typically provided by 2D pose estimators for each predicted 2D joint by including them into the 2D input vector as well as into the reprojection loss formulation.

Notably, this is without assuming any camera calibration or static cameras.

Method

우리의 approach는 two step으로 구성된다 : 첫째 기존의 2D joint detector에 input image를 넣는다, 그리고 두번째, 이 detections와 각 joint에 대한 각각의 confidences를 3D로 lifting한다.
우리 approach의 핵심 아이디어는 canonical pose space를 통해 one view에서 2D detections가 또 하나의 view에 projected 될 수 있게 하는것이다.
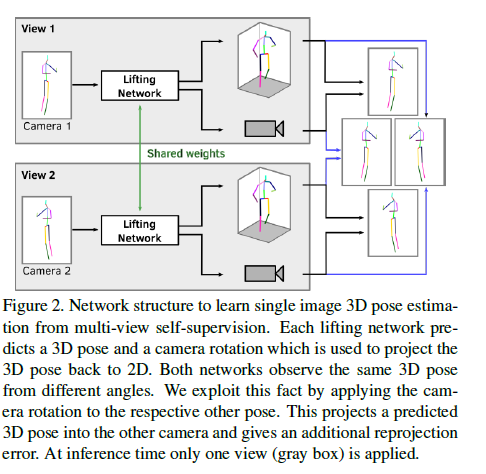
간단하게 network 구조는 오로지 2개의 cameras만 보여준다. 만약에 cameras가 더 사용가능하다면 곧장 확장할 수 있다. A single neural network, 3D lifting network는 3D pose \(X\)와 camera coordinate system의 pose로 rotate하기위해 rotation \(R\)을 예측한다.
Pose는 canonical pose 좌표계로 표현되고 이것은 training동안 자동으로 학습된다.
예측된 3D pose는 예측한 rotation에 의해 pose 좌표계에서 camera 좌표계로 rotated된다

Canonical human pose와 camera rotation간의 분리는 views들과 samples에 걸친 self-supervision에 다양한 reprojection losses를 공식화할 수 있게 한다.

3.1. Reprojection

2D pose를 3D로 lifting하기전에 그것을 root joint로 중심화 되어 normalized되고 Frobenius norm에 의해 나뉘어 scaled된다.
Monocular reconstruction에는 Scale-depth ambiguity가 있다.
Root joint를 centering하는 것은 모든 3D predictions를 위해 common rotation point 주는것이다.
각 view에서 예측된 3D pose는 RX에 의해 camera 좌표계로 rotated된다. \(R\)은 \(RR^T = I_3\)과 같은 rotational matrix이다, \(I_3\)은 3 x 3 identity matrix, \(det(R) = 1\). 우리는 weak perspective cameras를 가정하기 때문에, camera plane으로 projection은 간단히 depth coordinate를 제거함으로써 수행된다. \[W_{rep} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} RX\]

이것을 reprojected 2D pose라고 부른다. \(W\)는 실제 input인 2D pose. 그러면 scale-independent reprojection loss는 다음과 같이 정의한다. \(\mathcal{L}_{rep} = \begin{Vmatrix} W- \frac{W_{rep}}{\Vert W_{rep} \Vert_F} \end{Vmatrix}_{1}\)

3D pose의 global scale은 모르고 weak perspective projections를 고려하기 때문에 reprojection \(W_{rep}\) 를 scaling하는것은 필수적이다

이미 2D pose \(W\)는 전처리 과정중 Frobenius norm에 의해 나눠졌음. 이것은 input pose와 예측된 pose 모두 같은 scale이라는뜻이다. 따라서 원래 input 2D pose와 예측된 2D pose 모두 같은 scale로 만들어야함 근데 rotation을 예측하기위해서 matrix \(R\)을 직접 예측하지는 못하고 axis-angle representation으로 예측가능하다. \(θ\) 를 rotational angle이라 하고 \(w = (w1,w2,w3)\)가 rotation axis라고 하자. \[A = \begin{pmatrix} 0 & -w_3 & w2 \\ w_3 & 0 & -w_1 \\ -w_2 & w1 & 0 \end{pmatrix}\]

Rodrigues’ formula를 통해 rotation matrix를 얻는다.
\(R = I_3 + (sin \theta)A + (1- cos \theta)A^2\)

3.2. View-consistency

View consistency(일관성)을 보장하는 간단한 방법은 두개의 views에 의해 예측된 canonical poses간의 L2 loss를 적용하는 것이다. 이 이론에서, 서로 다른 views로부터 같은 사람 seen이 같은 canonical pose를 가져야하기 때문에 loss는 0이어야한다. 하지만 사실, 이것은 view 불변성이지만 더 이상 input pose에 밀접하게 대응하지 않는 lifting network learning 3D poses로 이어지고 network가 우리의 preliminary experiments에서 적절한 solutions로 수렴하는 것을 막는다.

제안된 method의 핵심 통찰은 서로 다른 views에서 rotations와 poses는 이전에 도입된 다양한 reprojection objective로서 view consistency를 강화하기 위해 mixed되어야 한다는 것이다.

우리는 예측된 카메라와 view-1과 view-2라 불리는 두개의 views의 pose를 source view-1에서 target view-2까지 view-2의 rotation을 사용함으로써 예측된 canonical 3D pose mix한다. 두개의 cameras는 4개의 가능한 rotations와 poses의 조합이 존재한다. 같은 방법으로 카메라가 m개로 늘리면 m^2개의 조합이 가능하다. Inference stage에서 lifting network는 single frame에 적용되고 다른 inputs가 필요하지 않다.

요약 : view consistency를 강화하기위해서 rotations와 poses가 mix되어야함. The key insight to the proposed method is that rotations and poses from different views can be mixed to enforce the view consistency as a variant of the previously introduced reprojection objective.

3.3. Confidence

대부분 pretrained 2D joint estimators의 output은 2D heatmaps이고 각 entry(항목)는 image에 관련 position에 해당하는 joint가 있는지 여부에 대한 confidence(신뢰도,자신감)를 나타낸다.
보통, argmax나 soft-argmax가 계산되고 다음 lifting network에 input으로 받는다. 하지만 이것은 정확한 joint position에 2D detection의 confidence의 independent를 준다. 그것은 불확실한 예측이 특정예측과 동일한 방식으로 진행된다는 것을 의미한다. 우리는 이 문제를 두개의 간단한 수정으로 우회한다.
첫째, 각 heatmap의 최대값, 즉 confidence의 대리 값와 2D pose input vector를 우리의 lifting network에 concatenate합니다.
두번째, input 2D pose와 reprojected 2D간의 각 차이는 그것의 confidence로 선형 가중되는 reprojection error를 수정한다. \[C = \begin{pmatrix} c_1 & c_2 & .. & c_j \\ c1 & c_2 & .. & c_j \end{pmatrix}\]

각 joint j에 대한 처는 joint j에서 heatmap의 최대값 \(L_{rep,c} = \begin{Vmatrix}(W - \frac{W_rep}{||W_rep||_F}) \odot C \end{Vmatrix}_1\) –> 즉 scaled된 pose \(W\)와 scaled된 reprojected pose \(W_{rep}\)의 차이의 confidence map의 요소 곱셈의 \(L_1\) norm

3.4 Camera-consistency

많은 motion capture setup에대한 합리적인 가정은 sequence가 기록되는 동안 cameras가 고정이다, 즉 카메라의 position이나 orientation이 변하지 않는다.
이런경우가 Human3.6M과 3DHP dataset에 있다.
그러나 이 가정은 제안된 방법에는 필수 사항이 아니라 정적 카메라를 사용하는 장면의 개선 사항이다.
카메라가 움직이는 SkiPose dataset에서 이것 없이 우리 approach의 performance 뿐만 아니라 실험에서 optional improvement에 영향을 주는 것을 보여준다.

Static camera setup에 대해, 카메라간의 모든 relative rotations은 같다.
Static camera를 강화하는 초기 approach는 training samples의 one batch에 걸친 relative rotations간의 L_2 loss를 계산하는것이다.
그러나 만일 a bath-wise loss의 weight가 low value로 설정되어있다면 a bath-wise loss는 degraded solutions를 이끌거나 영향을 주지않는다.
이러한 관찰은 Sec.3.2.의 canonical pose equality에 관한 findings와 유사하다.
이러한 이유로 우리는 Sec 3.2에서와 유사한 mixing approach을 제안한다. 이제 한 batch에서 서로 다른 샘플의 추정치를 초과한다.

Relative rotation \(R_{1,2}\)는 예측한 rotation matrix \(R_1\)과 \(R_2\)을 이용해서 다음과 같이 정의한다.
\(R_{1,2} = R_2R^T_1\)

\(R_{1,2}^{(s)}\) 를 sample \(s\)의 view-1과 view-2 사이의 predicted relative rotation이라고 하자. batch안에서 이 relative rotations를 무작위로 배치하고 Eq.1과 유사하게 canonical poses로 이것들을 reproject한다.
\(W_{rep} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \end{pmatrix} R_{1,2}^{(s)}R_{1}^{(s')}X^{(s')}\)

여기서 \(R_{1}^{(s')}\)와 \(X^{(s')}\)는 현재 frame에서 rotation과 예측한 3D pose 이고 \(R_{1,2}^{(s)}\)는 batch에서 또 하나의 sample로부터 randomly하게 할당된 relative rotation이다.
Loss는 Eq2에서 reprojection loss와 같은 방법으로 계산된다.
Sec3.2와 유사하게 이것은 쉽게 multiple cameras에 확장된다.
다시 강조하지만, static cameras의 경우 결과를 개선하기 위해서는 이 loss가 선택사항이다. 그러나 우리의 method는 이것 없이 작동한다.

3.5 Network Architecture

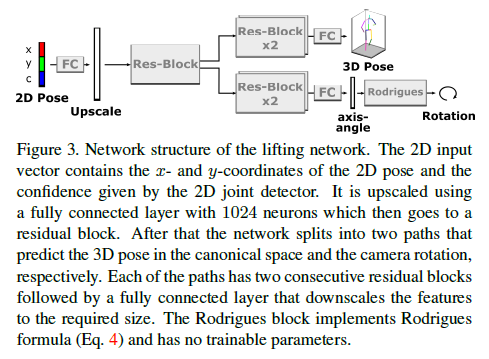
Fig3은 우리의 lifting network 구조를 보여준다.
Input 2D pose vector는 각 joint와 confidences를 포함하는 vector로 concatenated되어있다. 이것은 one fully connected layer에 의해 1024 neurons로 upscaled된다.
다음으로 dimension이 1024인 fully connected layers로 구성된 a residual block이 따라온다. Output은 2개의 path로 되어있는데 첫번째 residual block과 구분되는 각각 2개의 연속된 residual blocks을 통과한다.
3D pose path는 직접적으로 pose coordinate system에서 예측된 pose의 3D coordinates를 출력한다.
Camera path는 three-dimensional vector \(θω\) 이것은 axis angle representation이다.
Rotation matrix는 Rodrigues’ formula에 의해 계산된다. 마지막 2개 output layers를 제외하고 각 layer별 activation functions는 ReLU이고 negative slope는 0.01. initial learning rate of 0.0001을 갖는 Adam optimizer로 100 epochs로 network를 훈련하고 각 epochs별 weight decay는 각각 30,60,90이다.

4. Experiments

우리는 잘 알려진 benchmark datasets인 Human3.6M과 MPI-INF-3DHP에서 수행한다.
추가적으로 우리는 SkiPose dataset에서 evaluate하고 우리의 method가 real world scenarios에서도 일반적인지 test한다.
특정 활동 집합에 대해 레이블이 없는 이미지로 single image pose estimator를 training하는 설정을 준수하기 위해, 추가 데이터 세트를 사용하지 않고 각 데이터 세트에 대해 하나의 네트워크를 교육한다.

4.1 Metrics

Human3.6M에 evaluation을 위해 두개의 standard protocols가 있다.
Mean per joint position error (MPJPE), 즉, reconstructed joint coordinates와 ground truth joint coordinates 사이의 mean Euclidean distance이다.
Multi-view self-supervised setting은 metric data를 포함하고 있지 않기 때문에, 우리는 MPJPE를 계산하기 전에, 우리의 예측값의 scale을 조정한다.
다른 논문들과 공평한 비교를 위해 가능한 경우 scale adjusted predictions와 비교한다.
Protocol-I는 MPJPE를 직접적으로 계산한다.
Protocol-II는 poses간의 rigid alignment를 사용한다.
MPJPE 외에 3DHP용 protocol 1개가 the Percentage of Correct Keypoins(PCK)을 계산합니다.
이것은 ground truth joint기준 150mm 거리 이내에 예측한 joints의 percentage이다.

Correct Poses Score (CPS) 동작 분석 및 예측과 같은 실제 적용의 경우, 전체 pose의 평가가 중요한 전제 조건이다.
pose의 single joint가 부정확하더라도 downstream tasks이 크게 변경될 수 있다.
이전에 도입된 측정기준은 joint별 prediction의 품질을 평가한다.
그러나 poses에 대한 joints의 할당을 무시하고 대신 test set의 모든 joints에 대해 평균을 낸다. …. 이 section에서 우리는 이러한 경우 evaluate하기위해 간단하지만 강력한 metric, Correct Poses Score (CPS)를 제시한다.
Pose \(W\)는 만일 모든 joints \(i\)의 Euclidean distance가 threshold value \(θ\)이내라면 옳다고 고려된다.
Joint positions \(ω_i\) 와 예측된 joint positions \(\hat{ω}_i\) 라 하면 rigid alignment 이후에 옳은 pose는 다음과 같이 정의한다. \[CP_{\theta} = \begin{cases} 1 & \Vert w_i -\hat{w}_i \Vert_{2} < \theta \\ 0 & else \end{cases}\]

PMPJPE와 우리의 CP-metric 비교. 각 column 비교 서로 다른 예측된 3D reconstructions과 ground truth간의 비교. PMPJPE는 시각화 된 case에서 우측 arm에 위치한 high individual joint errors를 평균화하지만 CP는 이를 나타낸다.
이런 방법으로, 전반적인 pose의 옳음이 평가된다.
CPS의 계산을 위해 우리는 threshold를 변경하는데 예시로 180mm이다.
CPS는 \(θ∈[0mm,300mm]\)범위의 area under curve 넓이

4.2 Skeleton Morphing

우리는 우리의 model의 input으로 2D human pose estimation을 넣기 위해 off-the-shelf detector로 AlphaPose를 이용한다.
AlphaPose 훈련에 사용되는 datasets의 keypoint locations와 다른 2D pose estimation methods들이 test benchmarks의 3D skeleton이 다르다.
예를들어, root joint position은 hip joints의 중간에 있지 않고 목과 어깨의 상대적 위치가 다르다.
우리는 AlphaPose에서 dataset의 ground truth 2D pose까지 2D pose 사이의 차이를 예측하는 2D skeleton morphing network를 훈련함으로써 이런 문제를 우회한다.
우리는 각 dataset의 ground truth가 있는 subject1로 morphing network를 훈련한다.
이 ground truth는 3d pose model을 학습하는데는 사용되지않기위해서 subject1은 실험에서 완전 배제된다.
우리의 data는 self supervised training을 위해서만 사용되므로 어떤 2d ground truth는 포함되지 않는다.
Morphing network는 전혀 images를 보지 않고 그래서 domain specific image features를 학습할 수 없다.
skeletal structure는 다른 skeleton과 match할 필요가 없는 실험환경에서 이 단계는 할 필요는 없다.

4.3 Quantitative Evaluation on Human3.6M and 3DHP

Human3.6M dataset에서, 이전 approaches를 유지하기 위해, 우리는 standard protocols 를 따랐고 오로지 매 64번째 frame만 평가했다.
그러나 우리의 전체 pipeline의 bottle neck을 수행하는 충분히 빠른 2D pose estimator를 사용하면 실시간 성능을 달성할 수 있다.
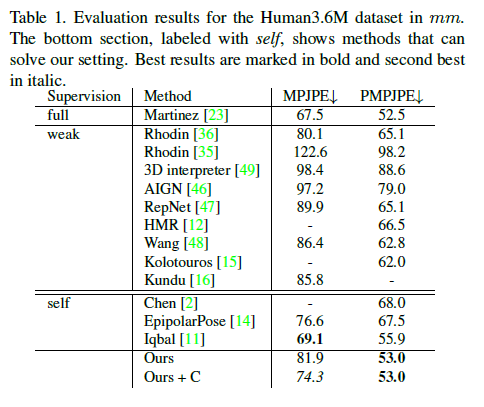
Table1은 제안한 method결과와 다른 Sota approaches들과 비교하여 보여준다. PMPJPE에서 다른 모든 approach와 비교하여 outperform한다.
Fully supervised method이며 단일 lifting하는 2017년 논문인 A simple yet effective baseline for 3d human pose estimation 논문과도 비교할만한 성능을 성취하였다.
분석 결과, pose structure가 매우 정확하지만(PMPJPE가 낮음) 오류의 가장 큰 부분은 rotation의 약간의 offset에서 비롯된다는 것이 밝혀졌다.
예를 들어, human3.6M dataset의 subject 9에서 frame 1과 세로 축을 중심으로 15도로 회전된것과 비교하면 이미 67.7mm의 MPJPE를 보여준다.
대부분의 methods들은 scene이나 어떤 3D training data가 작은 rotation은 작은 reprojection loss를 이끌지만 큰 3D MPJPE error를 이끌기 때문에 MPJPE와 PMPJPE간의 큰 차이를 보여줌을 모른다.
NVIDIAPOSE는 여전히 MPJPE에서 state of art이지만 그들은 training set의 ground truth 3D data로부터 직접적으로 계산되는 bone length constraints가 필요하다.
우리 approach는 skeletal structure에 어떤 predefined priors가 필요없다.
우리의 static camera constraint (Ours+C)를 사용하는 것은 MPJPE를 상당히 상승시킨다.
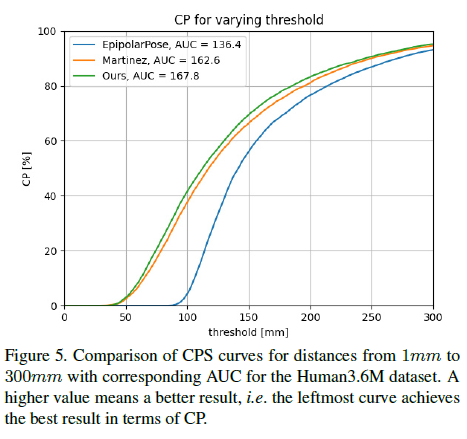
Fig.5는 우리 method와 EpipolarPose, 3D pose estimation baseline 모델의 CPS를 비교하여 보여준다. 우리는 EpipolarPose를 큰 margin으로 능가한다.
또한 우리는 우리의 approach를 3DHP dataset에 다음 standard test protocols와 metrics에 평가한다.
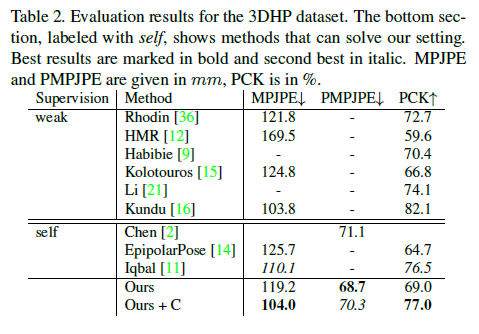
Table2는 그 결과를 보여준다.
우리는 다른 모든 self supervised approach를 능가하였다.
다른 approaches들과 대조적으로 제안한 method는 calibrated cameras나 anthropometric constraints를 요구하지않는다. CPS metric에서 우리는 134.2를 성취한다.

4.4 Moving cameras

우리의 주요 motivation은 temporally synchronized cameras에서 multi-view camera system을 이용해서 in the wild한 환경에서 3D human pose estimation이 가능하게 하는 것이다.
더욱이 수행된 activity 매우 capture하기 매우 어려울 수도 있도 전통적인 motion capture studio에서 수행하기 어려울 수도 있다.
즉, pretraining 또는 다른 데이터 세트와 결합된 훈련과 같은 직접적인 activity domain 전송은 합리적이지 않다.
SkiPose dataset은 이 motivation의 모든 도전이 들어있다.
이 대회에는 알파인 스키 선수들이 대회 전 run 하는 것이 특징이다.
이 데이터 세트를 기록하기 위해 카메라를 설정 및 보정하고 보정 후 카메라를 제자리에 유지하기 위해 많은 노력을 기울였다.
또한, 카메라는 알파인 스키어를 시야에 들어오게 하기 위해 회전하고 확대/축소했다.
제안된 방법은 calibrated 또는 static setup이 필요하지 않고 multiple synchronised cameras 와 함께 작동하기 때문에 이러한 모든 어려움을 처리할 수 있다.
camera setup이 static하지 않기 때문에 우리는 relative rotation constraint을 여기에 적용할 수 없다.
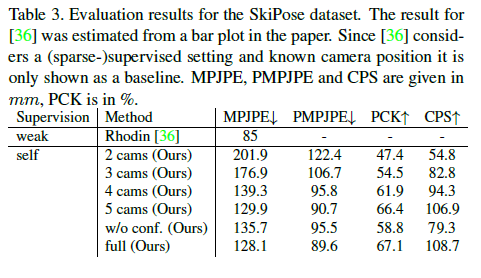
Table3은 SkiPose 논문과 비교하여 서로 다른 구성의 결과를 보여준다.
a (sparse-)supervised setting 과 known camera positions를 고려하기 때문에 direct comparison은 불가능하고 baseline으로서 제공한다.
Fig.6은 second row에서 SkiPose dataset의 qualitative results를 보여준다.

4.5. Ablation Studies

우리의 approach를 분석하기 위해, 우리는 많은 ablation studies를 수행한다.
첫째, 제한된 resources와 practical setting을 수행하기 위해, 우리는 model을 train하기위한 cameras 수를 줄인다.
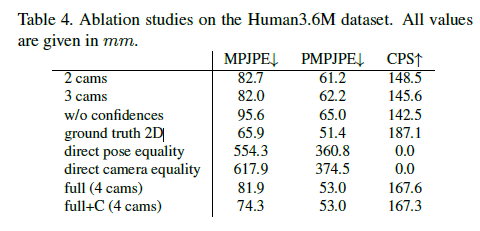
Table4와 Table3은 카메라 개수에 따른 training 결과를 보여준다.
Performance는 낮춘 training samples와 views 때문에 역시나 조금 떨어졌지만, 우리의 approach는 여전히 좋은 결과를 생산한다, 이것은 실세계 시나리오에 적용할수 있다.
두번째 실험에서 우리는 2D joint estimator에서 confidences를 network의 input으로 사용하는 것과 reprojection error 계산에 효과가 있음을 보여준다. 상당히 향상되었다. View-와 camera-consistency를 달성하기 위해 제안된 rotations와 poses를 mixing은 단순한 equality constraints보다 우수하다는 것을 증명하기위해, 이런 equality constraints를 가지고 실험을 수행했다.
그 결과는 우리의 mixing approach는 실제로 그것을 작동시키는 필수적인 부분임을 보여준다.
우리는 또한 [11]의 bone lengths constraints을 실험했지만 결과는 개선되지 않았다.
lower bound계산하기 위해서 ground truth 2D annotations와 함께 training 결과를 또한 보여준다.

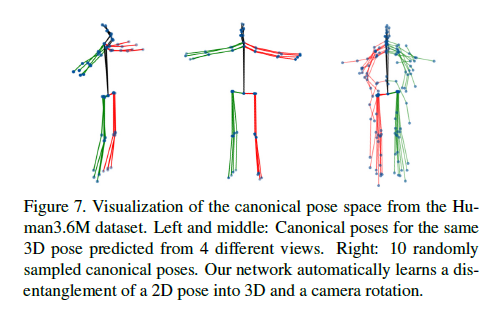
4.6. Are We Learning a Canonical Pose Basis?

마지막으로 우리는 우리가 canonical pose basis를 배운다는 주장을 평가한다.
다른 3D poses의 disentanglement(분리)를 시각화하기 위해 Fig.7은 왼쪽과 가운데의 4개의 views들에서 얻은 canonical basis로 재구성된 3D poses의 시각화를 보여준다.

오른쪽 이미지는 10개를 랜덤하게 뽑은 canonical space에서의 reconstructions들을 보여준다.
비록 poses의 유사성은 Sec3.2에서 설명한 것처럼 직접적으로 시행되지는 않지만 poses는 canonical space에서 비슷하게 방향이 잡혀있다.
특히, hip joints는 정렬되어있어 상체의 정렬이 비슷하다.
Human3.6M의 test set에서부터 canonical poses의 hip joints에 대한 표준편차(standard deviation)는 각각 오른쪽 왼쪽 hip에대해 7.9mm, 7.7mm이다.
Poses와 rotation은 우리 network에 의해 그럴듯하게 풀렸다.

5. Conclusion

우리는 single image 3D human pose estimation from multi-view data without 2D or 3D annotations를 학습하는 neural network인 CanonPose를 제시한다.
Pretrained 2D human pose estimator를 고려하여, 우리는 자동적으로 2D observation을 canonical 3D pose와 (mixing이후에 다시 observation으로 reproject하는데 사용되는)camera rotation으로 decompose하기위해 multi-view consistency를 사용한다.
우리의 approach는 multi-view data에 대해 2D나 3D annotations 모두 필요가 없기 때문에, 많은 움직이는 카메라의 outdoor장면을 포함하여 in-the-wild scenarios에서 적용될 수 있다.
우리는 benchmark datasets에 대해 다른 논문들과 비교하여 적은 사전요청임에도 sota를 달성했을 뿐만 아니라 challenging outdoor scenes에 대해서도 전망 있는 결과를 보여주었다.