Lightweight Multi-View 3D Pose Estimation through Camera-Disentangled Representation
.
Remelli, Edoardo, et al. “Lightweight multi-view 3d pose estimation through camera-disentangled representation.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020. paper
Abstract
We present a lightweight solution to recover 3D pose from multi-view images captured with spatially calibrated cameras.
Building upon recent advances in interpretable representation learning, we exploit 3D geometry to fuse input images into a unified latent representation of pose, which is disentangled from camera view-points.
This allows us to reason effectively about 3D pose across different views without using compute-intensive volumetric grids.
Our architecture then conditions the learned representation on camera projection operators to produce accurate per-view 2d detections, that can be simply lifted to 3D via a differentiable Direct Linear Transform (DLT) layer.
In order to do it efficiently, we propose a novel implementation of DLT that is orders of magnitude faster on GPU architectures than standard SVD-based triangulation methods.
We evaluate our approach on two large-scale human pose datasets (H36M and Total Capture): our method outperforms or performs comparably to the state-of-the-art volumetric methods, while, unlike them, yielding real-time performance.
1.Introduction
Most recent works on human 3D pose capture has focused on monocular reconstruction, even though multi-view reconstruction is much easier, since multi-camera setups are perceived as being too cumbersome.
The appearance of Virtual/ Augmented Reality headsets with multiple integrated cameras challenges this perception and has the potential to bring back multi-camera techniques to the fore, but only if multi-view approaches can be made sufficiently lightweight to fit within the limits of low-compute headsets.
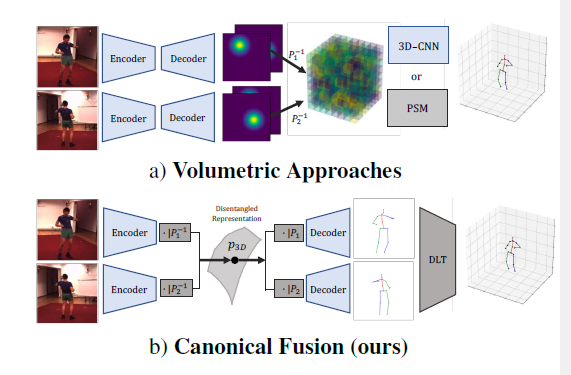
Unfortunately, the state-of-the-art multi-camera 3D pose estimation algorithms tend to be computationally expensive because they rely on deep networks that operate on volumetric grids [14], or volumetric Pictorial Structures [22, 21], to combine features coming from different views in accordance with epipolar geometry.
Fig. 1(a) illustrates these approaches.
In this paper, we demonstrate that the expense of using a 3D grid is not required.
Fig. 1(b) depicts our approach.
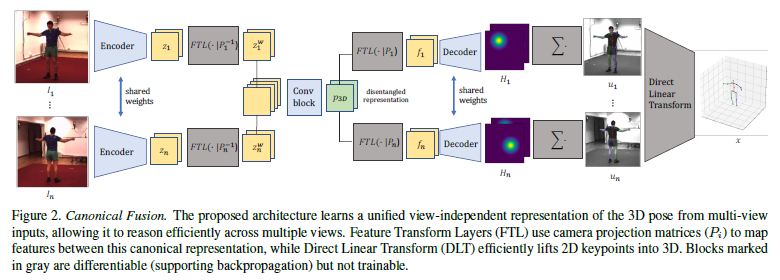
We encode each input image into latent representations, which are then efficiently transformed from image coordinates into world coordinates by conditioning on the appropriate camera transformation using feature transform layers [31].
This yields feature maps that live in a canonical frame of reference and are disentangled from the camera poses.
The feature maps are fused using 1D convolutions into a unified latent representation, denoted as $p_{3D}$ in Fig. 1(b), which makes it possible to reason jointly about the extracted 2D poses across camera views.
We then condition this latent code on the known camera transformation to decode it back to 2D image locations using a shallow 2D CNN.
The proposed fusion technique, to which we will refer to as Canonical Fusion, enables us to drastically improve the accuracy of the 2D detection compared to the results obtained from each image independently, so much so, that we can lift these 2D detections to 3D reliably using the simple Direct Linear Transform (DLT) method [11].
Because standard DLT implementations that rely on Singular Value Decomposition (SVD) are rarely efficient on GPUs, we designed a faster alternative implementation based on the Shifted Iterations method [23].
In short, our contributions are:
(1) a novel multi-camera fusion technique that exploits 3D geometry in latent space to efficiently and jointly reason about different views and drastically improve the accuracy of 2D detectors,
(2) a new GPU-friendly implementation of the DLT method, which is hundreds of times faster than standard implementations.
We evaluate our approach on two large-scale multi-view datasets, Human3.6M [13] and TotalCapture [29]: we outperform the state-of-the-art methods when additional training data is not available, both in terms of speed and accuracy.
When additional 2D annotations can be used [17, 2], our accuracy remains comparable to that of the state-of-the-art methods, while being faster.
Finally, we demonstrate that our approach can handle viewpoints that were never seen during training.
In short, we can achieve real-time performance without sacrificing prediction accuracy nor viewpoint flexibility, while other approaches cannot.
Figure 1. Overview of 3D pose estimation from multi-view images. The state-of-the-art approaches project 2D detections to 3D grids and reason jointly across views through computationally intensive volumetric convolutional neural networks [14] or Pictorial Structures (PSM) [22, 21]. This yields accurate predictions but is computationally expensive. We design a lightweight architecture that predicts 2D joint locations from a learned camera-independent representation of 3D pose and then lifts them to 3D via an efficient formulation of differentiable triangulation (DLT). Our method achieves performance comparable to volumetric methods, while, unlike them, working in real-time.
2.Related Work
Pose estimation is a long-standing problem in the computer vision community.
In this section, we review in detail related multi-view pose estimation literature.
We then focus on approaches lifting 2D detections to 3D via triangulation.
Pose estimation from multi-view input images.
Early attempts [18, 9, 4, 3] tackled pose-estimation from multiview inputs by optimizing simple parametric models of the human body to match hand-crafted image features in each view, achieving limited success outside of the controlled settings.
With the advent of deep learning, the dominant paradigm has shifted towards estimating 2D poses from each view separately, through exploiting efficient monocular pose estimation architectures [20, 28, 30, 26], and then recovering the 3D pose from single view detections.
Most approaches use 3D volumes to aggregate 2D predictions.
Pavlakos et al. [21] project 2D keypoint heatmaps to 3D grids and use Pictorial Structures aggregation to estimate 3D poses.
Similarly, [22] proposes to use Recurrent Pictorial Structures to efficiently refine 3D pose estimations step by step.
Improving upon these approaches, [14] projects 2D heatmaps to a 3D volume using a differentiable model and regresses the estimated root-centered 3D pose through a learnable 3D convolutional neural network.
This allows them to train their system end-to-end by optimizing directly the 3D metric of interest through the predictions of the 2D pose estimator network.
Despite recovering 3D poses reliably, volumetric approaches are computationally demanding, and simple triangulation of 2D detections is still the de-facto standard when seeking real-time performance [16, 5].
Few models have focused on developing lightweight solutions to reason about multi-view inputs.
In particular, [15] proposes to concatenate together pre-computed 2D detections and pass them as input to a fully connected network to predict global 3D joint coordinates.
Similarly, [22] refines 2D heatmap detections jointly by using a fully connected layer before aggregating them on 3D volumes.
Although, similar to our proposed approach, these methods fuse information from different views without using volumetric grids, they do not leverage camera information and thus overfit to a specific camera setting.
We will show that our approach can handle different cameras flexibly and even generalize to unseen ones.
Triangulating 2D detections.
Computing the position of a point in 3D-space given its images in \(n\) views and the camera matrices of those views is one of the most studied computer vision problems.
We refer the reader to [11] for an overview of existing methods.
In our work, we use the Direct Linear Triangulation (DLT) method because it is simple and differentiable.
We propose a novel GPU-friendly implementation of this method, which is up to two orders of magnitude faster than existing ones that are based on SVD factorization.
We provide a more detailed overview about this algorithm in Section 3.4.
Several methods lift 2D detections efficiently to 3D by means of triangulation [1, 16, 10, 5].
More closely related to our work, [14] proposes to back-propagate through an SVD-based differentiable triangulation layer by lifting 2D detections to 3D keypoints.
Unlike our approach, these methods do not perform any explicit reasoning about multi-view inputs and therefore struggle with large self-occlusions.
3.Method
We consider a setting in which \(n\) spatially calibrated and temporally synchronized cameras capture the performance of a single individual in the scene. We denote with \({I_i}^n_{i=1}\) the set of multi-view input images, each captured from a camera with known projection matrix \(P_i\). Our goal is to estimate its 3D pose in the absolute world coordinates; we parameterize it as a fixed-size set of 3D point locations \(\{x^j\}^J_{j=1}\), which correspond to the joints.
Consider as an example the input images on the left of Figure 2. Although exhibiting different appearances, the frames share the same 3D pose information up to a perspective projection and view-dependent occlusions. Building on this observation, we design our architecture (depicted in Figure 2), which learns a unified view-independent representation of 3D pose from multi-view input images. This allows us to reason efficiently about occlusions to produce accurate 2D detections, that can be then simply lifted to 3D absolute coordinates by means of triangulation. Below, we first introduce baseline methods for pose estimation from multi-view inputs. We then describe our approach in detail and explain how we train our model.
3.1. Lightweight pose estimation from multiview inputs
Given input images \({I_i}^n_{i=1}\), we use a convolutional neural network backbone to extract features \({z_i}^n_{i=1}\) from each input image separately. Denoting our encoder network as \(e\), \(z_i\) is computed as \(z_i = e(T_i). \tag{1}\)
Note that, at this stage, feature map \(z_i\) contains a representation of the 3D pose of the performer that is fully entangled with camera view-point, expressed by the camera projection operator \(P_i\).
We first propose a baseline approach, similar to [16, 10], to estimate the 3D pose from multi-view inputs. Here, we simply decode latent codes \(z_i\) to 2D detections, and lift 2D detections to 3D by means of triangulation. We refer to this approach as Baseline. Although efficient, we argue that this approach is limited because it processes each view independently and therefore cannot handle self-occlusions.
An intuitive way to jointly reason across different views is to use a learnable neural network to share information across embeddings \(\{z_i\}^n_{i=1}\), by concatenating features from different views and processing them through convolutional layers into view-dependent features, similar in spirit to the recent models [15, 22]. In Section 4 we refer to this general approach as Fusion. Although computationally lightweight and effective, we argue that this approach is limited for two reasons: (1) it does not make use of known camera information, relying on the network to learn the spatial configuration of the multi-view setting from the data itself, and (2) it cannot generalize to different camera settings by design. We will provide evidence for this in Section 4 .
3.2. Learning a viewindependent representation
To alleviate the aforementioned limitations, we propose a method to jointly reason across views, leveraging the observation that the 3D pose information contained in feature maps \({z_i}^n_{i=1}\) is the same across all n views up to camera projective transforms and occlusions, as discussed above. We will refer to this approach as Canonical Fusion.
To achieve this goal, we leverage feature transform layers (FTL) [31], which was originally proposed as a technique to condition latent embeddings on a target transformation so that to learn interpretable representations. Internally, a FTL has no learnable parameter and is computationally efficient. It simply reshapes the input feature map to a point-set, applies the target transformation, and then reshapes the point-set back to its original dimension. This technique forces the learned latent feature space to preserve the structure of the transformation, resulting in practice in a disentanglement between the learned representation and the transformation. In order to make this paper more self-contained, we review FTL in detail in the Supplementary Section.
Several approaches have used FTL for novel view synthesis to map the latent representation of images or poses from one view to another [25, 24, 7, 6]. In this work, we leverage FTL to map images from multiple views to a unified latent representation of 3D pose. In particular, we use FTL to project feature maps zi to a common canonical representation by explicitly conditioning them on the camera projection matrix P−1 i that maps image coordinates to the world coordinates \(z^w_i = \text{FTL}(z_i|P^{-1}_i). \tag{2}\)
Now that feature maps have been mapped to the same canonical representation, they can simply be concatenated and fused into a unified representation of 3D pose via a shallow 1D convolutional neural network \(f\), i.e. \(p_{3D} = f(concatenate(\{z^w_i\}^n_{i=1})). \tag{3}\)
We now force the learned representation to be disentangled from camera view-point by transforming the shared \(p_3D\) features to view-specific representations \(f_i\) by \(f_i = \text{FTL}(p_{3D}|P_i). \tag{4}\)
In Section 4 we show both qualitatively and quantitatively that the representation of 3D pose we learn is effectively disentangled from the camera-view point.
Unlike the Fusion baseline, Canonical Fusion makes explicit use of camera projection operators to simplify the task of jointly reasoning about views. The convolutional block, in fact, now does not have to figure out the geometrical disposition of the multi-camera setting and can solely focus on reasoning about occlusion. Moreover, as we will show, Canonical Fusion can handle different cameras flexibly, and even generalize to unseen ones.
